Bonjour, suite à une idée que j'ai eue, j'aimerai savoir comment déterminer les coordonnées du centre de gravité G d'un demi-cercle.
Pour cela, soit

la fonction dont la courbe représentative
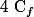
dans un repère direct orthonormé
)
est définie par :
=\sqrt{1-(x-1)^2})
Je conjecture tout de suite que
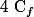
dans
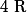
admet pour axe de symétrie la droite d'équation
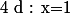
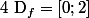
.
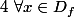
:
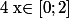
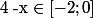
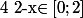
donc
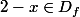
et
=\sqrt{1-((2-x)-1)^2}=\sqrt{1-(1-x)^2}=f(x))
Par conséquent,
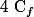
admet bien la droite
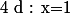
pour axe de symétrie.
Mon idée en fait est que si on considère G le centre de gravité de ce demi-cercle et l'aire
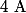
définie par
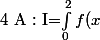 \quad dx)
alors
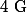
vérifie
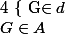
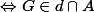
i.e.
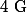
appartient à
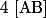
tq
)
et
)
Donc déjà,
)
, mais comment trouver son ordonnée ?
Je pense qu'il faudrait peut-être calculer la valeur moyenne de f sur [0;2], non ?
