Bonjour, j'aurai besoin de quelqu'un pouvant m'aider pour résoudre un énoncé; le voici :
On considère la suite (Wn) définie sur N par : Wn = 2^n/n²
Calculer est simplifier Wn+1 - Wn
Pour le moment en classe nous avons mis uniquement ceci :
Wn+1-Wn=2^n+1 /(n+1)²-2^n /n²
De mon coté j'ai pensé faire :
2^n+1*n²-2^n*(n+1)²/(n+1)²*n²
j'aurai voulu savoir si cela est juste, si oui que dois-je faire après? et si non, que dois-je faire à la place?
Merci d'avance pour votre aide !
Calculer et simplifier une suite
28 messages
- Page 1 sur 2 - 1, 2
par C.Ret » 28 Nov 2012, 17:50
Bonsoir.
Bon, soit il va falloir penser à utiliser des parenthèses, soit utiliser la mise en forme des équations TEX parceque sinon c'est illisible.
De plus il faut rédiger plus rigoureusement, en particulier je ne comprends pas à quoi correspond la dernière expression ?
C'est
?
Et donc je suis bien incapable de dire si c'est juste ou faux !
Bon, soit il va falloir penser à utiliser des parenthèses, soit utiliser la mise en forme des équations TEX parceque sinon c'est illisible.
De plus il faut rédiger plus rigoureusement, en particulier je ne comprends pas à quoi correspond la dernière expression ?
C'est
Et donc je suis bien incapable de dire si c'est juste ou faux !
par annick » 28 Nov 2012, 17:55
Bonjour,
jusqu'à présent c'est juste.
On peut envisager que 2^(n+1)=(2^n)(2) (en vertu de x^(a+b)=(x^a)(x^b) )
On pourra donc factoriser par 2^n.
On peut aussi développer (n+1)²
Et à la fin, on pourra arranger tout ça.
jusqu'à présent c'est juste.
On peut envisager que 2^(n+1)=(2^n)(2) (en vertu de x^(a+b)=(x^a)(x^b) )
On pourra donc factoriser par 2^n.
On peut aussi développer (n+1)²
Et à la fin, on pourra arranger tout ça.
par C.Ret » 28 Nov 2012, 18:04
annik vous êtes un grand magicien, ou un voyant extra lucide ?
Pour vous :
2^n+1*n²-2^n*(n+1)²/(n+1)²*n²
Est équivalent à
^2}{(n+1)^2.n^2})
Comment vous faites ?
Pour vous :
2^n+1*n²-2^n*(n+1)²/(n+1)²*n²
Est équivalent à
Comment vous faites ?
par Carpate » 28 Nov 2012, 18:06
LittleChat a écrit:Bonjour, j'aurai besoin de quelqu'un pouvant m'aider pour résoudre un énoncé; le voici :
On considère la suite (Wn) définie sur N par : Wn = 2^n/n²
Calculer est simplifier Wn+1 - Wn
Pour le moment en classe nous avons mis uniquement ceci :
Wn+1-Wn=2^n+1 /(n+1)²-2^n /n²
De mon coté j'ai pensé faire :
2^n+1*n²-2^n*(n+1)²/(n+1)²*n²
j'aurai voulu savoir si cela est juste, si oui que dois-je faire après? et si non, que dois-je faire à la place?
Merci d'avance pour votre aide !
qui est
par LittleChat » 28 Nov 2012, 18:09
C.Ret a écrit:annik vous êtes un grand magicien, ou un voyant extra lucide ?
Pour vous :
2^n+1*n²-2^n*(n+1)²/(n+1)²*n²
Est équivalent à
Comment vous faites ?
Oui je sais que j'aurais dû mieux rédiger, mais je ne savais comment le faire sur ce forum. désolé. :/
par LittleChat » 28 Nov 2012, 18:16
annick a écrit:Bonjour,
jusqu'à présent c'est juste.
On peut envisager que 2^(n+1)=(2^n)(2) (en vertu de x^(a+b)=(x^a)(x^b) )
On pourra donc factoriser par 2^n.
On peut aussi développer (n+1)²
Et à la fin, on pourra arranger tout ça.
pour le développement :
(n+1)² = n²+2n+1 c'est ça?
par contre je n'ai pas réellement compris pour le reste, je mets énormément de temps à comprendre (surtout qu'à la fin je dois savoir le refaire)
par C.Ret » 28 Nov 2012, 18:48
OUi,
Le plus simple et de reprendre depuis le début :
^2}\;-\; \frac{2^n}{n^2})
L'idée de mettre au même dénominateur est excellente, on multiplie donc le terme de gauche par
et celui de droite par ^2)
On obtient :
^2}{n^2[/COLOR].(n+1)^2})
Occupons nous explusivement du numérateur :
^2)
Dans un premier temps, nous cherchons à factoriser par
.
Pour cela nous transformons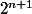
en 
On a alors :
^2\\<br />N\;=\;2^n.\left( 2.n^2\;-\;(n+1)^2 \right))
A ce point, come il n'y a pas de simplification évidente, on développe/
 \right))
)
)
On a donc :
}{n^2.(n+1)^2})
^2}\right))
EDIT: J'ai corrigé le n^2 dont le 2 manquait ! Mea Culpa.
Le plus simple et de reprendre depuis le début :
L'idée de mettre au même dénominateur est excellente, on multiplie donc le terme de gauche par
On obtient :
Occupons nous explusivement du numérateur :
Dans un premier temps, nous cherchons à factoriser par
Pour cela nous transformons
On a alors :
A ce point, come il n'y a pas de simplification évidente, on développe
On a donc :
EDIT: J'ai corrigé le n^2 dont le 2 manquait ! Mea Culpa.
par LittleChat » 28 Nov 2012, 18:50
et avec ce qu'il a fait, je dois simplifier ou faire autre chose après ? ou je dois laisser comme Carpate a fait?
ah oui! il faut aussi que je détermine le signe (donc si c'est croissant) si j'ai bien compris pour le signe, il faut regarder le nomre devant n non?
ah oui! il faut aussi que je détermine le signe (donc si c'est croissant) si j'ai bien compris pour le signe, il faut regarder le nomre devant n non?
par LittleChat » 28 Nov 2012, 18:53
C.Ret a écrit:OUi,
Le plus simple et de reprendre depuis le début :
L'idée de mettre au même dénominateur est excellente, on multiplie donc le terme de gauche par
On obtient :
Occupons nous explusivement du numérateur :
Dans un premier temps, nous cherchons à factoriser par
Pour cela nous transformons
On a alors :
A ce point, come il n'y a pas de simplification évidente, on développe
On a donc :
MERCI BCP JE COMMENCE A MIEUX COMPRENDRE!
par LittleChat » 28 Nov 2012, 19:11
j'ai oublié de te demander, est-ce que je dois encore calculer ou simplifier ou que c'est la fin?
et comment je fais pour déterminer le signe du coup? parce que je suis perdue avec tous les n. :(
et comment je fais pour déterminer le signe du coup? parce que je suis perdue avec tous les n. :(
par Carpate » 29 Nov 2012, 14:41
LittleChat a écrit:j'ai oublié de te demander, est-ce que je dois encore calculer ou simplifier ou que c'est la fin?
et comment je fais pour déterminer le signe du coup? parce que je suis perdue avec tous les n.
C'est un peu décourageant avec toi.
Tu donnes l'impression que tu ne lis même pas nos messages !
Je reprends mon premier message :
Si j''ai isolé volontairement
Comment établir le signe de
par C.Ret » 29 Nov 2012, 14:59
LittleChat a écrit:MERCI BCP JE COMMENCE A MIEUX COMPRENDRE!
Dommage que ce ne soit que le début. Parceque que ce qui est interressant avec le savoir et la science et justement de finir par comprendre.
par LittleChat » 29 Nov 2012, 17:19
C.Ret a écrit:OUi,
Le plus simple et de reprendre depuis le début :
L'idée de mettre au même dénominateur est excellente, on multiplie donc le terme de gauche par
On obtient :
Occupons nous explusivement du numérateur :
Dans un premier temps, nous cherchons à factoriser par
Pour cela nous transformons
On a alors :
A ce point, come il n'y a pas de simplification évidente, on développe
On a donc :
bon j'ai compris pas mal le début sauf que je viens de me rendre compte qu'à ton avant dernière ligne de calcul :
Or si j'ai bien suivi l'avant dernière ligne serait :
non? peut etre que je me trompe ou que je n'ai pas bien suivi mais bon..
par annick » 29 Nov 2012, 17:31
Ce doit être une erreur d'étourderie, mais oui, je te confirme que tu as bien suivi et c'est bien n².
par Carpate » 29 Nov 2012, 17:36
annick a écrit:Ce doit être une erreur d'étourderie, mais oui, je te confirme que tu as bien suivi et c'est bien n².
Oui, c'est un simple oubli de C.Ret : errare humanum est
par annick » 29 Nov 2012, 17:40
c'est sûr et ça peut rassurer les élèves de savoir que ça arrive effectivement à tout le monde :lol3:
par C.Ret » 29 Nov 2012, 17:46
annick a écrit:c'est sûr et ça peut rassurer les élèves de savoir que ça arrive effectivement à tout le monde :lol3:
Cela m'arrive même plus souvent qu'à mon tour.
C'est bien une erreur d'étourderie.
Je dirais à ma décharge que le codage en TEX des formules est peu lisible.
Et vous me répondrez que j'avais qu'à me relire !
Vous avez raison !
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :