bonjour à tous, pourriez vous m'aider à calculer les primitives de ces fonctions suivantes qui me donnent du fil à retordre:
f(x)=cos^2 (x)
et
g(x)=(sin^2 x)/cos^2 (x)+ 2
je ne vois pas du tout comment faire , quelles formules utilisées.
Une idée?? Merci de vôtre aide!
Calcul primitives cosinus au carré TS
8 messages
- Page 1 sur 1
par Ericovitchi » 10 Mai 2009, 18:32
Il faut se rappeler ses formules de trigo quand on veut intégrer
=\frac{1+cos(2x)}{2})
par RG2 » 10 Mai 2009, 19:19
merci pour la formule, mais je ne comprends pas comment vous avez fait pour l'obtenir.
par busard_des_roseaux » 11 Mai 2009, 08:08
Bonjour,
=1+tan^2(x)=\frac{1}{cos^2(x)})
pour la (2)
1er cas
si=tan^2(x)+2)
, c'est résolu.
2ème cas
si=\frac{sin^2(x)}{cos^2(x)+2})
=\frac{tan^2(x)}{3+tan^2(x)})
ce qui revient à primitiver avec la variable
=\frac{u^2}{(3+u^2)(1+u^2)})
avec 
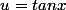
or
(1+u^2)}=\frac{3}{2(3+u^2)} - \frac{1}{2(1+u^2)})
pour la (2)
1er cas
si
2ème cas
si
ce qui revient à primitiver avec la variable
or
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :