Bon j'ai tjrs des problèmes avec le barycentre et ses demonstrations et y a un exercice que j'arrive pas à resoudre et j''aimerai de l'aide.
On considère un parallelogramme ABCD et deux points M et N tel que M est le barycentre de (A,2) et (B,1) et N est le barycentre de (C,2) et (B,1) . Montrer que (AC) // (MN)
j'ai essayé avec la relation de charles ma je n'ai rien trouvé ;/
Barycentre
10 messages
- Page 1 sur 1
Salut !
 est le barycentre de
est le barycentre de ) et
et ) donc quel que soit le point
donc quel que soit le point  du plan,
du plan, 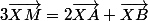 .
.
De même pour le barycentre , quel que soit X,
, quel que soit X, 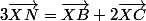 .
.
En remarquant que, d'après la relation de Chasles, quel que soit ,
, 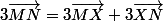 , justifie que les vecteurs
, justifie que les vecteurs 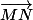 et
et  sont colinéaires.
sont colinéaires.
:+++:
De même pour le barycentre
En remarquant que, d'après la relation de Chasles, quel que soit
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
asmaaae_x a écrit:oui :/ J'avais introduis chaque point mais rien ne marchais pour moi!
Je pense qu'il voulait souligner le nom que porte cette relation :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
