Salut tout le monde,
J’ai mon bac dans 1 semaine environ et j’aimerais comprendre la démonstration pas récurrence, démontrer qu’une suite est croissante, déduire qu’une suite est convergente ou divergente et bien d’autres si vous connaissez
Je vous remercie d’avance et j’espère que vous pourrez le venir en aide
Bac : Besoin d’aide pour les suites
7 messages
- Page 1 sur 1
Re: Bac : Besoin d’aide pour les suites
Bonjour,
il y a plein d'infos sur le net.
A toi de voir les explications qui éclairent "ta lanterne" et qui te permettent d'y voir plus clair
il y a plein d'infos sur le net.
A toi de voir les explications qui éclairent "ta lanterne" et qui te permettent d'y voir plus clair
Re: Bac : Besoin d’aide pour les suites
Salut je vous remercie de votre réponse rapide
Pour l’exercice j’ai d’énorme difficulté pour le raisonnement par récurrence en effet je n’arrive pas à comprendre les démarches à suivre lors de l’hérédité je ne sais pas ce qu’il faut faire à ce moment là
Pour l’exercice j’ai d’énorme difficulté pour le raisonnement par récurrence en effet je n’arrive pas à comprendre les démarches à suivre lors de l’hérédité je ne sais pas ce qu’il faut faire à ce moment là
Re: Bac : Besoin d’aide pour les suites
Ok mais dans cet exercice c'est vraiment sans difficultés !
On suppose que pour un entier n quelconque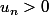
et on doit démontrer que cette même propriété est aussi vraie pour l'indice suivant c'est à dire que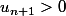
On suppose que pour un entier n quelconque
et on doit démontrer que cette même propriété est aussi vraie pour l'indice suivant c'est à dire que
Re: Bac : Besoin d’aide pour les suites
Recurence:
Si c'est vraie Pn au rang n alors c'est aussi vrai au rang n+1 Pn+1 est aussi vraie.
Une suite est croissante:
Géométrique si Un+1/Un>0 convergente si valeur absolue de la raison <1
Arithmétique si Un+1-Un>0
Si c'est vraie Pn au rang n alors c'est aussi vrai au rang n+1 Pn+1 est aussi vraie.
Une suite est croissante:
Géométrique si Un+1/Un>0 convergente si valeur absolue de la raison <1
Arithmétique si Un+1-Un>0
Re: Bac : Besoin d’aide pour les suites
Bonjour,
Divergente si valeur absolue de la raison >1 pour des suites géométrique si raison >0 pour des suites arithmétiques.
Divergente si valeur absolue de la raison >1 pour des suites géométrique si raison >0 pour des suites arithmétiques.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

