Applications du produit scalaire.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
extasy
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2009, 22:56
-
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 08 Avr 2010, 20:13
par Arnaud-29-31 » 08 Avr 2010, 20:13
Bonsoir,
Il faut aller chercher les bonnes formules de trigo.
Pour le a) , quelle est la formule toute bête qui lie cos(x) et sin(x) ?
b) On peut exprimer cos(2x-y) en fonction de cos(x), sin(x), cos(y) et sin(y) ...
-
extasy
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2009, 22:56
-
 par extasy » 08 Avr 2010, 20:27
par extasy » 08 Avr 2010, 20:27
Pour le a, j'ai utilisé : cos²(x)+sin²(x)=1 donc sin(x) =
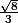
et sin(y) =
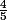
.
-
extasy
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2009, 22:56
-
 par extasy » 08 Avr 2010, 20:31
par extasy » 08 Avr 2010, 20:31
Pour la question b, je ne vois pas comment exprimer cos(2x-y) en fonction de cos(x), sin(x), cos(y) et sin(y)...
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 08 Avr 2010, 20:33
par ned aero » 08 Avr 2010, 20:33
salut
une des formules de duplication (cours)
cos(a - b)= cosa*cosb + sina*sinb
ps: ;)8 = 2;)2 pour le a)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 08 Avr 2010, 20:34
par Arnaud-29-31 » 08 Avr 2010, 20:34
Oui, c'est ça.
Et pour la b) on peut utiliser les formules :
cos(a+b) = cos(a).cos(b) - sin(a).sin(b)
cos(a-b) = cos(a).cos(b) + sin(a).sin(b)
sin(a+b) = sin(a).cos(b) + sin(b).cos(a)
cos(a-b) = sin(a).cos(b) - sin(b).cos(a)
-
extasy
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2009, 22:56
-
 par extasy » 08 Avr 2010, 21:00
par extasy » 08 Avr 2010, 21:00
Ah oui !
Donc ça donne : cos(2x-y) = cos(2x)cos(y)+sin(2x)sin(y)
Et après le cos(2x) il faut remplacer par quoi ? cos²(x)-sin²(x) ?
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 08 Avr 2010, 21:05
par ned aero » 08 Avr 2010, 21:05
oui c'est ça
-
extasy
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2009, 22:56
-
 par extasy » 08 Avr 2010, 21:22
par extasy » 08 Avr 2010, 21:22
Donc j'arrive à :
cos(2x-y) = (cos²(x)-sin²(x))cos(y)+(2cos(x)sin(x))sin(y)
Il faut développer ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 08 Avr 2010, 21:36
par Arnaud-29-31 » 08 Avr 2010, 21:36
Y'a pas grand chose à développer là ...
Tu remplace juste les cos et les sin par leurs valeurs numériques ...
-
extasy
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2009, 22:56
-
 par extasy » 09 Avr 2010, 18:10
par extasy » 09 Avr 2010, 18:10
Pour cos(2x-y) je trouve :
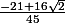
et pour sin(2x-y) je trouve :
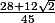
.
Voilà.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités