Bonjour,
Je ne comprends pas pourquoi avec pour une fonction f : E --> F, si E est vide alors il existe une application que l'on appelle " application vide " et si F est vide alors il n'y a pas d'application.
Pourquoi y en a t-il une dans un cas et pas dans l'autre?
Question stupide sûrement... Mais bon, c'est comme ça que l'on avance...
Application vide
8 messages
- Page 1 sur 1
Aloha,
Il faut revenir aux bases : une application, c'est une partie de ExF, telle qu'il y ait un unique couple de la forme (e, qqchose) pour tout e dans E.
Si E est vide, il existe bien une partie de ExF qui vérifie ça : l'ensemble vide (qui correspond à l'application vide)
Si E n'est pas vide, et que F est vide : tu prends un e dans E (tu peux, E est non vide). Tu ne peux pas mettre dans ton application un couple de la forme (e, qqchose), vu qu'il n'existe aucun "qqchose".
Donc il n'y a pas d'application de E dans Vide.
Par contre, si E et F sont vides, il y a une (et une seule) application de E dans F.
Il faut revenir aux bases : une application, c'est une partie de ExF, telle qu'il y ait un unique couple de la forme (e, qqchose) pour tout e dans E.
Si E est vide, il existe bien une partie de ExF qui vérifie ça : l'ensemble vide (qui correspond à l'application vide)
Si E n'est pas vide, et que F est vide : tu prends un e dans E (tu peux, E est non vide). Tu ne peux pas mettre dans ton application un couple de la forme (e, qqchose), vu qu'il n'existe aucun "qqchose".
Donc il n'y a pas d'application de E dans Vide.
Par contre, si E et F sont vides, il y a une (et une seule) application de E dans F.
« Je ne suis pas un numéro, je suis un homme libre ! »
Salut,
et merci pour cette réponse.
Juste une précision, si tu as encore un peu de temps...
"Si E est vide, il existe bien une partie de ExF qui vérifie ça : l'ensemble vide"
La je comprends pas trop... ExF, c'est tous les couples (e,f) tel que e appartienne à E et f à F. L'ensemble vide n'est pas un couple, non?
Pour le reste j'ai compris!
et merci pour cette réponse.
Juste une précision, si tu as encore un peu de temps...
"Si E est vide, il existe bien une partie de ExF qui vérifie ça : l'ensemble vide"
La je comprends pas trop... ExF, c'est tous les couples (e,f) tel que e appartienne à E et f à F. L'ensemble vide n'est pas un couple, non?
Pour le reste j'ai compris!
La modestie s'apprend par la répétition de l'échec.
mathelot a écrit:
En tant qu'ensemble , le produit cartésien ExF admetcomme partie.
Ah d'accord! Je viens de comprendre le truc...
Je bloquais car je ne pouvais pas concevoir qu'un couple soit un ensemble. Bref... Cela m'a d'ailleurs amené à faire quelques recherches et à tomber sur cette définition d'un couple ( a,b ):
Le couple ( a,b ), c'est l'ensemble {{a},{a,b}}.
En fait, c'est juste le " codage ensembliste " qui vérifie la propriété fondamentale des couples.
La modestie s'apprend par la répétition de l'échec.
Salut,
Pour comprendre que, si E est vide alors ExF est vide, il n'est absolument pas nécessaire de voir les couples comme des ensembles (a mon sens c'est même plutôt nocif).
Tu ne cherche pas à montrer que l'ensemble vide est un élément de ExF, c'est à dire que l'ensemble vide est un couple (ce qui est systématiquement faux), mais à montrer que l'ensemble ExF est vide, c'est à dire qu'il ne contient aucun élément.
C'est totalement différent vu que si l'ensemble vide était effectivement un élément de ExF, ben ça prouverais en particulier que ExF est non vide !!!
Pour te donner l'exemple le plus con qui me vient à l'esprit, c'est si E= alors E est vide, son cardinal est 0 et il ne contient aucun éléments. Donc, par exemple
alors E est vide, son cardinal est 0 et il ne contient aucun éléments. Donc, par exemple  est faux (à évidement à ne pas confondre avec
est faux (à évidement à ne pas confondre avec 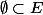 qui lui est vrai et qui est même vrai pour tout nsemble E, vide ou pas)
qui lui est vrai et qui est même vrai pour tout nsemble E, vide ou pas)
Par contre, toujours avec E= , on a P(E)={
, on a P(E)={ } qui est cette fois non vide vu que
} qui est cette fois non vide vu que  est un (et même le seul) élément de P(E). DOnc le cardinal de P(E) est 1 et c'est (heureusement) cohérent avec la formule générale que dit que, si le cardinal de E est n alors celui de P(E) est 2^n (ici n=0 et 2^n=1)
est un (et même le seul) élément de P(E). DOnc le cardinal de P(E) est 1 et c'est (heureusement) cohérent avec la formule générale que dit que, si le cardinal de E est n alors celui de P(E) est 2^n (ici n=0 et 2^n=1)
Sinon, concernant ton truc, c'est complètement con : les éléments de ExF, c'est les couples (x,y) avec x dans E et y dans F donc si E (ou F) est vide, tu ne peut former aucun couple et donc ExF est vide.
Si tu veut mon opinion, tout ça semble vouloir dire que tu n'as pas encore totalement "digéré" la différence essentielle entre les notions d'appartenance et d'inclusion
et d'inclusion 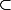 .
.
Pour faire des tests (pourris s'il en est),
1) Peut tu me donner A et B tels qu'on ait a la fois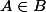 et
et 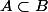 ?
?
2) Peut tu me donner A et B tels qu'on ait a la fois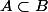 et
et 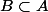 ?
?
3) Peut tu me donner A et B tels qu'on ait a la fois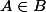 et
et  ?
?
alexis6 a écrit:Je bloquais car je ne pouvais pas concevoir qu'un couple soit un ensemble.
Pour comprendre que, si E est vide alors ExF est vide, il n'est absolument pas nécessaire de voir les couples comme des ensembles (a mon sens c'est même plutôt nocif).
Tu ne cherche pas à montrer que l'ensemble vide est un élément de ExF, c'est à dire que l'ensemble vide est un couple (ce qui est systématiquement faux), mais à montrer que l'ensemble ExF est vide, c'est à dire qu'il ne contient aucun élément.
C'est totalement différent vu que si l'ensemble vide était effectivement un élément de ExF, ben ça prouverais en particulier que ExF est non vide !!!
Pour te donner l'exemple le plus con qui me vient à l'esprit, c'est si E=
Par contre, toujours avec E=
Sinon, concernant ton truc, c'est complètement con : les éléments de ExF, c'est les couples (x,y) avec x dans E et y dans F donc si E (ou F) est vide, tu ne peut former aucun couple et donc ExF est vide.
Si tu veut mon opinion, tout ça semble vouloir dire que tu n'as pas encore totalement "digéré" la différence essentielle entre les notions d'appartenance
Pour faire des tests (pourris s'il en est),
1) Peut tu me donner A et B tels qu'on ait a la fois
2) Peut tu me donner A et B tels qu'on ait a la fois
3) Peut tu me donner A et B tels qu'on ait a la fois
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Pour comprendre que, si E est vide alors ExF est vide, il n'est absolument pas nécessaire de voir les couples comme des ensembles (a mon sens c'est même plutôt nocif).
Tu ne cherche pas à montrer que l'ensemble vide est un élément de ExF, c'est à dire que l'ensemble vide est un couple (ce qui est systématiquement faux), mais à montrer que l'ensemble ExF est vide, c'est à dire qu'il ne contient aucun élément.
C'est totalement différent vu que si l'ensemble vide était effectivement un élément de ExF, ben ça prouverais en particulier que ExF est non vide !!!
Pour te donner l'exemple le plus con qui me vient à l'esprit, c'est si E=alors E est vide, son cardinal est 0 et il ne contient aucun éléments. Donc, par exemple
est faux (à évidement à ne pas confondre avec
qui lui est vrai et qui est même vrai pour tout nsemble E, vide ou pas)
Par contre, toujours avec E=, on a P(E)={
} qui est cette fois non vide vu que
est un (et même le seul) élément de P(E). DOnc le cardinal de P(E) est 1 et c'est (heureusement) cohérent avec la formule générale que dit que, si le cardinal de E est n alors celui de P(E) est 2^n (ici n=0 et 2^n=1)
Sinon, concernant ton truc, c'est complètement con : les éléments de ExF, c'est les couples (x,y) avec x dans E et y dans F donc si E (ou F) est vide, tu ne peut former aucun couple et donc ExF est vide.
Si tu veut mon opinion, tout ça semble vouloir dire que tu n'as pas encore totalement "digéré" la différence essentielle entre les notions d'appartenanceet d'inclusion
.
Pour faire des tests (pourris s'il en est),
1) Peut tu me donner A et B tels qu'on ait a la foiset
?
2) Peut tu me donner A et B tels qu'on ait a la foiset
?
3) Peut tu me donner A et B tels qu'on ait a la foiset
?
Salut,
1) Ca me semble pas possible parce que cela implique que A soit à la fois un objet mathématique et un ensemble.
2) A=B={x}
3) Même remarque que pour le 1)
Apparement, j'avais toujours pas compris... Merci pour cette deuxième explication.
La modestie s'apprend par la répétition de l'échec.
alexis6 a écrit:1) Ca me semble pas possible parce que cela implique que A soit à la fois un objet mathématique et un ensemble.
2) A=B={x}
3) Même remarque que pour le 1)
Apparement, j'avais toujours pas compris... Merci pour cette deuxième explication.
Correction :
1) c'est tout à fait possible, par exemple A=
On peut aussi donner des exemples moins subtils :
A={ 3 , {2,3} } et B={ 1 , 3 , {1,2} , {2,3} , {1,{2,3}} , {{1}} }
On a bien
On a bien
2) oui, A=B={x} marche et même (et c'est très important) "
3) Là, c'est super compliqué : dans le modèle standard des maths., à savoir celui de Zermelo-Fraenkel (ZF en abrégé) il y a un axiome (Axiome de fondation) qui dit effectivement que c'est impossible d'avoir
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
