Bonjour.
Je n'arrive pas à résoudre ce problème malgré mes nombreuses tentatives.
C'est un DM sur la dérivation.
Le problème (1ereS) :
Dans un repère orthonormé (O,I,J) , on donne le A (3;2)
M est un point de coordonnées (x;0) avec x>3
La droite (AM) coupe l'axe des ordonnées en N de coordonnées (0;y) avec y>2
Déterminer la position exacte de M pour laquelle l'aire du triangle ON est minimale
Merci d'avance.
Anthony
Application de la dérivation : un triangle d'aire minimale
5 messages
- Page 1 sur 1
Re: Application de la dérivation : un triangle d'aire minima
Je n'arrive pas à résoudre ce problème malgré mes nombreuses tentatives.
C'est un DM sur la dérivation.
Il s'agit d'établir l'expression de l'aire A(x) du triangle ONM
L'aire de ce triangle sera extremun pour la valeur de x qui annule la dérivée A'(x)
Dans tes nombreuses tentatives , tu as quand même essayé de trouver une équation de la droite AM.
Que trouves-tu ?
L'intersection de cette droite avec l'axe des ordonnées te donnera les coordonnées du point N
Edit
Ce qui est un peu dérangeant c'est d'appeler x l'abscisse du point M tu peux la changer en m pour ne pas la confondre avec la variable x de l'équation de MN
A(x) deviendra alors A(m)
Modifié en dernier par Carpate le 11 Fév 2019, 17:23, modifié 5 fois.
Re: Application de la dérivation : un triangle d'aire minima
Oui effectivement je suis arrivé à trouver ça mais je ne comprend pas comment trouver une équation pour trouver l'aire du triangle. ON et OM doivent bien pouvoir se faire remplacer par quelque chose mais je ne sais pas quoi... 

Re: Application de la dérivation : un triangle d'aire minima
Soit A(3;2) et M(m;0)
L'équation réduite de AM vérifie :
de AM vérifie :
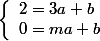
système de 2 équations aux 2 inconnues a et b dont tu tires a et b
L'équation réduite
système de 2 équations aux 2 inconnues a et b dont tu tires a et b
Re: Application de la dérivation : un triangle d'aire minima
Carpate a écrit:L'aire de ce triangle sera extremum pour la valeur de x qui annule la dérivée A'(x)
Dans la mesure où la dérivée seconde {A')'=A'' ne change pas de signe dans un voisinage de cette valeur.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
