
Analyse: suites: TS
23 messages
- Page 1 sur 2 - 1, 2
Analyse: suites: TS
:we: Bonjour, je voudrais bien de l'aide pour les exercices suivants. Une amie me les a envoyés par mail et je voudrais bien les faire mais, le problème c'est que je n'y arrive pas vraiment, je n'aime pas trop les suites. :hum: Par conséquent, je voudrais bien de votre aide. Merci d'avance. :happy2:


Bonjour,
1). , car
, car  .
.
On suppose que , c'est-à-dire que 5x_n-y_n+3=0.
, c'est-à-dire que 5x_n-y_n+3=0.
On vérifie donc que :
:
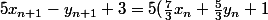-(\frac{20}{3}x_n+\frac{8}{3}y_n+5)+3) .
.
Je te laisse vérifier que cela fait bien 0.
Donc .
.
On a donc la relation : 5x_n-y_n+3=0, soit y_n = 5x_n+3.
Tu calcules en remplaçant
en remplaçant  par cette formule.
par cette formule.
2). Par récurrence: (clairement, vu que
(clairement, vu que 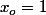 ).
).
Si , alors
, alors  , qui est égal à
, qui est égal à  ,
,  aussi.
aussi.
De même pour (soit en passant par y_n=5x_n+3, soit en calculant
(soit en passant par y_n=5x_n+3, soit en calculant 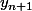 en fonction de
en fonction de  et en itérant le raisonnement par récurrence que tu viens de faire sur
et en itérant le raisonnement par récurrence que tu viens de faire sur  ).
).
3). a). Si 3 divise , on peut écrire
, on peut écrire 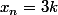 , pour un certain k.
, pour un certain k.
Donc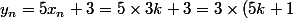) .
.
Donc est divisible par 3.
est divisible par 3.
Réciproquement, si 3 divise , alors il existe k' tel que
, alors il existe k' tel que  = 3k'.
= 3k'.
Donc .
.
 est un entier, et 3 divise
est un entier, et 3 divise  .
.
On a bien l'équivalence.
1).
On suppose que
On vérifie donc que
Je te laisse vérifier que cela fait bien 0.
Donc
On a donc la relation : 5x_n-y_n+3=0, soit y_n = 5x_n+3.
Tu calcules
2). Par récurrence:
Si
De même pour
3). a). Si 3 divise
Donc
Donc
Réciproquement, si 3 divise
Donc
On a bien l'équivalence.
Bonjour,
1). , car
, car  .
.
On suppose que , c'est-à-dire que 5x_n-y_n+3=0.
, c'est-à-dire que 5x_n-y_n+3=0.
On vérifie donc que :
:
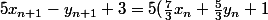-(\frac{20}{3}x_n+\frac{8}{3}y_n+5)+3) .
.
Je te laisse vérifier que cela fait bien 0.
Donc .
.
On a donc la relation : 5x_n-y_n+3=0, soit y_n = 5x_n+3.
Tu calcules en remplaçant
en remplaçant  par cette formule.
par cette formule.
2). Par récurrence: (clairement, vu que
(clairement, vu que 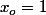 ).
).
Si , alors
, alors  , qui est égal à
, qui est égal à  ,
, 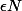 aussi.
aussi.
De même pour (soit en passant par y_n=5x_n+3, soit en calculant
(soit en passant par y_n=5x_n+3, soit en calculant 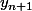 en fonction de
en fonction de  et en itérant le raisonnement par récurrence que tu viens de faire sur
et en itérant le raisonnement par récurrence que tu viens de faire sur  ).
).
3). a). Si 3 divise , on peut écrire
, on peut écrire 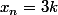 , pour un certain k.
, pour un certain k.
Donc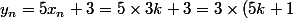) .
.
Donc est divisible par 3.
est divisible par 3.
Réciproquement, si 3 divise , alors il existe k' tel que
, alors il existe k' tel que  = 3k'.
= 3k'.
Donc .
.
 est un entier, et 3 divise
est un entier, et 3 divise  .
.
On a bien l'équivalence.
1).
On suppose que
On vérifie donc que
Je te laisse vérifier que cela fait bien 0.
Donc
On a donc la relation : 5x_n-y_n+3=0, soit y_n = 5x_n+3.
Tu calcules
2). Par récurrence:
Si
De même pour
3). a). Si 3 divise
Donc
Donc
Réciproquement, si 3 divise
Donc
On a bien l'équivalence.
Bonsoir, est-ce que vous pouvez me donner au moins quelques pistes pour les 2 exercices? J'espère que cela ne vous dérange pas de m'aider un peu mais, je voudrais bien progresser au niveau des exercices sur les suites car, j'ai quelques difficultés avec ce genre d'exercices et que j'ai bientôt un contrôle dessus. Merci beaucoup. :triste: :triste:
PS Elsa_toup: je crois que vos réponses ne sont pas sur le bon topic mais, qu'elles devraient aller sur l'autre topic que j'avais fais le même jour et ou je viens de préciser mes difficultés avant de voir que vous aviez mis des réponses ici.
PS Elsa_toup: je crois que vos réponses ne sont pas sur le bon topic mais, qu'elles devraient aller sur l'autre topic que j'avais fais le même jour et ou je viens de préciser mes difficultés avant de voir que vous aviez mis des réponses ici.
Bonjour, je voudrais bien de l'aide pour les questions que je n'arrive pas à faire. Voici un récapitulatif de ce que j'ai réussi à faire.
Pour l'exercice 1, j'ai trouvé pour la première question.
Pour l'exercice 2, j'ai trouvé pour la première question, pour la question 2, j'ai réussi à le prouver au rang 0 mais pas au rang n+1 et pour la question 3, je pense que normalement sa tend vers 0 quand n tend vers +l'infini mais, je n'arrive pas à l'expliquer.
Pour l'exercice 1, j'ai trouvé pour la première question.
Pour l'exercice 2, j'ai trouvé pour la première question, pour la question 2, j'ai réussi à le prouver au rang 0 mais pas au rang n+1 et pour la question 3, je pense que normalement sa tend vers 0 quand n tend vers +l'infini mais, je n'arrive pas à l'expliquer.
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
