Aire

par **jonathan93** » 06 Déc 2006, 15:52

Bonjour, je n'arrive pas à déterminer x.

j'ai trouvé les aires mais je n'y arrive pas.

On considere un demi-cercle de diamètre [AC], tel que AC = 16 cm
B est un point de [AC] et on note AB = 2x

Déterminer x pour que l'aire hachurée soit égale à l'aire restante (ici en rouge) .

par **jeps** » 06 Déc 2006, 16:00

et bien tu as fait le plus dur!!
il suffit de dire que la somme des aires vertes est égale à la somme de l'aire rouge, et après, c'est une simple résolution d'équation!

par **andros06** » 06 Déc 2006, 16:05

Aire totale = 32*pi (1)
Aire occupé par bleu = pi/2*{x^2+(8-x)^2} (2)
Aire restante (rouge)= (1)-(2) (3)

Il te reste à résoudre (2)=(3). Tu trouveras x=4 normalement.

Bonne chance dans tes calculs

par **jonathan93** » 06 Déc 2006, 16:20

J'ai essayé encore et encore.
Je n'arrive pas à trouver 4 :triste:

par **andros06** » 06 Déc 2006, 16:50

Aire totale = 32*pi (1)
Aire occupé par bleu = pi/2*{x^2+(8-x)^2} (2)
Aire restante (rouge)= (1)-(2) (3)

Il te reste à résoudre (2)=(3). Tu trouveras x=4 normalement.

Bonne chance dans tes calculs

quand tu fais (2)=(3) , tu obtiens l'équation suivante :

soit , après simplification :

Le calcul du discriminant te donne :

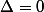
Donc tu as une racine double qui est

C'est tout

Aire

Aire

Qui est en ligne