1ere S : Barycentres de 4 points pondérés et plus..

[Ptite-rockeuse]

Bonsoir ! J'espère que vous profitez pleinement de votre jour férié !

J'aurais besoin d'aide pour un exercice de maths que j'ai à faire pour vendredi.. Je pense avoir des idées, mais je me demande si elles sont justes et si je peux ainsi aboutir à quelque chose !
Donc voici tout d'abord l'énoncé :

ABCD est un carré de centre O.

1. Montrer que C=bar{(A;-1)(B;1)(D;1)}

2. On pose S={(A;1)(B;2)(C;1)(D;-2)}
Montrer que {(B;3)(D;-1)} et S ont le même barycentre.

3. En déduire que G, barycentre du système S, est le symétrique de O par rapport à B. Construire le point G.

4. Montrer que pour tout point M du plan, le vecteur :
vecV= vecMA + 2vecMB - vecMC - 2vecMD
est indépendant du point M.

5. Déterminer et construire l'ensemble des points M du plan tels que vecV et vecMA + 2vecMB - vecMC - 2vecMD sont colinéaires.


Et voici ce que j'ai fait :

1. -1+1+1 différent de 0 donc C existe.

AC = 1AB + 1AD donc C=bar{(A;-1)(B;1)(D;1)}.

2. Je pensais passer par l'associativité :
Si S={(A;1)(B;2)(C;1)(D;-2)} et {(B;3)(D;-1)}
alors : {(G;2)(B;2)(D;-2)}
Mais après je suis bloquée

Ou sinon : Supposons G=bar{(B;3)(D;-1)}
alors : BG = -1/2BD
Et supposons G=bar{(A;1)(B;2)(C;1)(D;-2)}
alors : AG= -1AB + 1/2AC - 1AD.

Mais là encore, ça ne montre rien..

Pour la 3, il me faudrait répondre correctement à la 2, ce qui n'est pas le cas.
Et pour la 4 et la 5, je ne comprends pas tout à la relation fondamentale, comment s'en servir, à quoi sert-elle.. Mon cours est confus dessus, et je n'ai pas de définition précise, du coup je n'arrive pas à l'appliquer lors d'un exercice.

J'espère avoir fourni tous les éléments nécessaires, et merci à ceux qui m'apporteront de l'aide !
Bonne fin de soirée.

[zerkel]

bonsoir,
en fait pour t'en sortir tu écris la propriété qui te dis que pour C tu as pour tout point M
On va dire que tu appelles G le barycentre de S.
Tu écris ce que ça veut dire :
et tu te sers de la propriété du dessus avec un point M bien choisi.

[Ptite-rockeuse]

Donc dire que MC=-MA+MB+MD suffit pour prouver que C=bar{(A;-1)(B;1)(D;1)} et ensuite pour s'en servir à la question 2 ?
Et la solution que j'avais proposée n'est-elle pas correcte ? Solution qui permettait de placer le point C et donc de prouver ainsi son existence.

Par contre, je ne comprends pas comment faire la relation avec l'expression GA+2GB+GC-2GD=vec0 et la propriété du point M..

Comme je l'ai dit plus haut, je ne comprends quasiment rien à la relation fondamentale donc il m'est impossible d'appliquer quoi que ce soit ! Est-ce que tu pourrais me l'expliquer en quelques mots, quelle est son utilité ?
Je ne veux pas être embêtante mais mon envie est de vraiment bien comprendre pour ensuite réussir mes exercices.

[zerkel]

là je répondais à la question 2).
En fait tu vas utiliser la propriété fondamentale en M=G et remplacer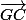 dans la formule à l'avant dernière ligne de mon message précédent.
Tu arriveras après simplification à la relation qui signifie que G est le barycentre de {(B;3)(D;-1)}.

Le meilleur moyen de prouver que C=bar{(A;-1)(B;1)(D;1)} c'est encore de prouver que .

[liliou]

salut,
esxuse moi, mais après est - ce que tu avais compris comment fait-on le barycentre de Quatre point pondérés parce que moi je fais plein de technique mais je ne trouve jamais la même chose.