Barycentre de 3 points pondérés

[bapt34]

Bonjour est ce que vous pourriez m'expliquer comment faire
ABCD est un parallélogramme
Déterminer 3 réels alpha béta et gamma de sorte que D soit le barycentre de (A,alpha) (B,béta) (C,gamma).
Merci d'avance.

[Imod]

Il suffit de transformer légèrement l'égalité : .

Imod

[c pi]

Bonjour

Pour que soit le barycentre de ,
il faut que sans oublier les conditions sur les coefficients ;
donc

Comme ABCD est un parallélogramme, ;
donc

Avec ces deux expressions de , on doit pouvoir trouver trois coefficients convenables.

[bapt34]

Oui mais je ne voix pas comment trouver les coefficients.

[c pi]

Dans les deux expressions du même vecteur ,
les coefficients multipliant chacun des vecteurs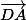 et 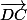doivent être égaux.
Tu dois trouver trois réels tels que... on ne te demande pas de déterminer tous les réels tels que...
Alors tu peux choisir une valeur pour un coefficient, celles des deux autres s'en déduiront à l'aide des égalités mises en évidence avec les deux expressions de