Tas de cailloux
Olympiades mathématiques, énigmes et défis
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 12 Mai 2007, 15:10
par Huit » 12 Mai 2007, 15:10
Bonjour à tous,
Je viens soumettre à votre sagacité une petite énigme qui traîne en ce moment dans les couloirs de mon internat. Je n'ai pas encore la réponse, je suis en phase de recherche mais je vourais tout de même la partager en espérant qu'elle n'est pas déjà était postée.
On dispose d'une pile de
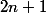
cailloux.
Chaque cailloux est associé à un poids

.
Lorsque l'on prend un cailloux quelconque de la pile, il est toujours possible de partager le tas restant en 2 tas de même poids et de

cailloux.
Prouver que tous les cailloux on le même poids.
Bonne chance.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 12 Mai 2007, 16:02
par Imod » 12 Mai 2007, 16:02
Bonjour,
c'est un problème classique souvent exposé avec des vaches à la place des cailloux . Il existe une solution utilisant les matrices mais il me semble qu'il y a des solutions plus simples ( niveau lycée ) si on impose aux masses d'être rationnelles ou entières .
Imod
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 12 Mai 2007, 16:36
par Flodelarab » 12 Mai 2007, 16:36
Imod a écrit:c'est un problème classique souvent exposé avec des vaches à la place des cailloux .
J'ai rarement vu une pile de vaches ....
Du moins rarement une pile de plus de 2 vaches ....
:ptdr:
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 12 Mai 2007, 16:43
par Huit » 12 Mai 2007, 16:43
Si quelqu'un connait une réponse matricielle je suis preneur.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 12 Mai 2007, 16:46
par Flodelarab » 12 Mai 2007, 16:46
Ça dépend. Tu veux les vidéos ?
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 12 Mai 2007, 16:53
par Imod » 12 Mai 2007, 16:53
Je m'absente 5 min et ça dégénère , il n'est pas possible ce forum :triste:
Pour les ames sensibles ou prudes , empiler les vaches n'est pas une obligation mais si on en choisit une , on peut faire deux paquets de même masse avec celles qui restent , elles peuvent alors jouer tranquillement au rami , tricoter , broder , ...
Imod
-
Riemann
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2007, 13:43
-
 par Riemann » 14 Mai 2007, 22:54
par Riemann » 14 Mai 2007, 22:54
Huit a écrit:Bonjour à tous,
Je viens soumettre à votre sagacité une petite énigme qui traîne en ce moment dans les couloirs de mon internat. Je n'ai pas encore la réponse, je suis en phase de recherche mais je vourais tout de même la partager en espérant qu'elle n'est pas déjà était postée.
On dispose d'une pile de
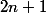
cailloux.
Chaque cailloux est associé à un poids

.
Lorsque l'on prend un cailloux quelconque de la pile, il est toujours possible de partager le tas restant en 2 tas de même poids et de

cailloux.
Prouver que tous les cailloux on le même poids.
Bonne chance.
commençons par reformuler le problème en langage mathématique:
Soit

le poids du caillou i.
Posons

.
On a

pour tout i
Ensuite, on somme les
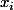
, et on obtient:
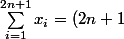x_{i})
.
Donc


etc.
et à la fin, on aboutit à

.
Ainsi

.
CQFD
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mai 2007, 06:32
par Quidam » 15 Mai 2007, 06:32
Riemann a écrit:Ensuite, on somme les
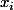
, et on obtient:
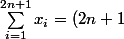x_{i})
.
Je n'ai pas compris ta démonstration ! C'est quoi le "i" du second membre ?
-
scelerat
- Membre Relatif
- Messages: 397
- Enregistré le: 03 Aoû 2005, 13:37
-
 par scelerat » 16 Mai 2007, 15:55
par scelerat » 16 Mai 2007, 15:55
Huit a écrit:Si quelqu'un connait une réponse matricielle je suis preneur.
Je ne connais pas la reponse, mais j'imagine que si on cherche des equations donnant le poids des cailloux, on en a 2n+1 avec chacune n coefficients a 1 et n a -1 pour exprimer l'egalite des deux sous-sommes. Donc, Il va y avoir un systeme lineaire dont chaque ligne comporte un zero dans une colonne differente, n fois 1 et n fois -1, et dont par hypothese le determinant est nul. Il suffirait de montrer qu'on a un sous-determinant de rang 2n non nul pour garantir que la solution triviale est unique.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Mai 2007, 18:40
par Imod » 16 Mai 2007, 18:40
C'est ça scelerat , reste à prouver que le rang de la matrice est bien 2n .
Imod
-
Riemann
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2007, 13:43
-
 par Riemann » 16 Mai 2007, 23:07
par Riemann » 16 Mai 2007, 23:07
Quidam a écrit:Je n'ai pas compris ta démonstration ! C'est quoi le "i" du second membre ?
je me suis trompée, c'était un "1" et pas un "i".
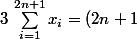x_{1})
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 17 Mai 2007, 23:44
par Quidam » 17 Mai 2007, 23:44
Riemann a écrit:commençons par reformuler le problème en langage mathématique:
Soit

le poids du caillou i.
Posons

.
On a

pour tout i
Ensuite, on somme les
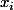
, et on obtient:
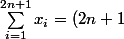x_{1})
.
Donc


etc.
et à la fin, on aboutit à

.
Ainsi

.
CQFD
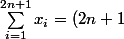x_{1})
????
Ah bon ! Eh qu'est-ce qui t'autorise à dire ça ? Je ne comprends toujours pas ! D'ailleurs je ne vois pas non plus à quel endroit de ta démonstration tu aurais utilisé l'hypothèse selon laquelle "Lorsque l'on prend un cailloux quelconque de la pile, il est toujours possible de partager le tas restant en 2 tas de même poids et de n cailloux." !!!!!!!!!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 19 Mai 2007, 01:51
par Joker62 » 19 Mai 2007, 01:51
Pas mal l'énoncé :ptdr::ptdr::ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
