Suite de rationnel

par **Nightmare** » 26 Oct 2007, 20:27

Bonsoir :happy3:

Je vous soumets un petit exo sympathique dont la/les démonstrations sont très jolies.

On considère deux suites

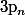
et

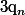
d'entiers telles que

admet une limite irrationnelle.

Question : Montrer que

.

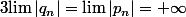
A vous de jouer.

par **yos** » 26 Oct 2007, 20:53

Salut.
Je vois ça comme ça :
Avec un entier q compris entre 1 et M, il n'y a qu'un nombre fini de p tels que

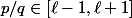
et aucun de ces p/q ne vaudra

. Donc en prenant

assez petit, aucun des p/q ne sera dans

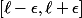
. Et donc l'inégalité

.
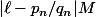
Mais l'inégalité

.
Pour

, ensuite c'est évident.

par **Nightmare** » 26 Oct 2007, 22:38

Salut Yos.

Je n'avais pas vu ça comme ça, je réfléchis à ta preuve. D'autres amateurs sinon?

par **ThSQ** » 27 Oct 2007, 07:42

Nightmare a écrit:D'autres amateurs sinon?

La preuve de yos est tout à fait valable. D'ailleurs c'est celle de mon bouquin

par **Imod** » 27 Oct 2007, 08:01

J'ai bien une démo mais elle paraît trop simple pour être juste :doh:

Si par exemple

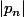
ne tend pas vers

alors

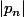
a une valeur d'adhérence dans

. On peut extraire de

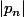
une suite constante

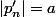
, la suite extraite

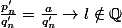
donc

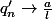
et

: c'est impossible .

Imod

par **Nightmare** » 27 Oct 2007, 15:04

Je n'ai pas dit que la preuve de Yos n'était pas bonne (pas assez prétentieux pour ça :lol:)

Oui Imod, c'est ma première preuve.