Suite contractante
Olympiades mathématiques, énigmes et défis
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Déc 2010, 20:46
par benekire2 » 04 Déc 2010, 20:46
Soit u une suite vérifiant
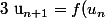)
telle que

avec f une application de R dans R telle que
 \in \mathbb{R}^2 |f(x)-f(y)|<|x-y|)
Etudier la convergence de u.
Bon travail !
PS . Je sais pas si ça mérite sa place ici ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Déc 2010, 21:08
par girdav » 04 Déc 2010, 21:08
On peut regarder par exemple pour la fonction
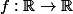
définie par
 =\sqrt{x^2+1})
.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 04 Déc 2010, 21:47
par Sylviel » 04 Déc 2010, 21:47
Je penses que
 \in \mathbb{R}^2 |f(x)-f(y)|\leq k|x-y|)
Est plus adapté...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Déc 2010, 21:56
par Ben314 » 04 Déc 2010, 21:56
Je voterais plutôt pour :

telle que
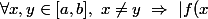-f(y)|<|x-y|)
qui est un peu plus rigolo.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 04 Déc 2010, 21:58
par Sylviel » 04 Déc 2010, 21:58
Oui, mais je ne sais pourquoi je pensais être dans la section lycée. Où ça me semblait violent.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Déc 2010, 22:02
par Ben314 » 04 Déc 2010, 22:02
Même niveau Lycée, c'est quand même pas la mer à boire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
darkpseudo
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Juil 2010, 16:22
-
 par darkpseudo » 04 Déc 2010, 22:22
par darkpseudo » 04 Déc 2010, 22:22
Ben314 a écrit:Je voterais plutôt pour :

telle que
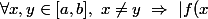-f(y)|<|x-y|)
qui est un peu plus rigolo.
Bonsoir , si f admet un point fixe on remplace y par ce point on remplace x par Un et en multipliant les termes et passant à la limite on obtient lim Un = y ( le point fixe ) c'est un truc d'école , mais si f n'admet pas de point fixe on fait comment stp ?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Déc 2010, 22:49
par benekire2 » 04 Déc 2010, 22:49
darkpseudo a écrit:Bonsoir , si f admet un point fixe on remplace y par ce point on remplace x par Un et en multipliant les termes et passant à la limite on obtient lim Un = y ( le point fixe ) c'est un truc d'école , mais si f n'admet pas de point fixe on fait comment stp ?
Et bien on montre qu'il y en a forcement un. .. Avec l enonce de ben bien sur.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Déc 2010, 23:04
par Ben314 » 04 Déc 2010, 23:04
darkpseudo a écrit:...en multipliant les termes et passant à la limite on obtient lim Un = y ( le point fixe )
tst sts sts, ce n'est pas aussi trivial que ça...
La suite Vn=|Un-L| est strictement décroissante et évidement minorée par 0 donc elle converge vers un certain lambda.
Mais pourquoi lambda est il forcément nul ?
Pour l'existence du point fixe, cela découle du fait que les hypothèses faites sur f impliquent que f est continue, que f(a)-a>=0 et que f(b)-b<=0 d'où...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 04 Déc 2010, 23:09
par kasmath » 04 Déc 2010, 23:09
on peux la liée à théorème de suite de Cauchy

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Déc 2010, 23:44
par Ben314 » 04 Déc 2010, 23:44
kasmath a écrit:on peux la liée à théorème de suite de Cauchy
On pourrait, mais ce n'est pas du tout obligatoire ici...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Déc 2010, 23:49
par benekire2 » 04 Déc 2010, 23:49
Perso je suppose que |a-f(a)| est le minimum de cette quantite et ensuite je suppose que a ne vaut pas f(a) et j en deduit assez rapidement une contradictiob pour ainsi montrer que ce point fixe existe, et il est clairement unique.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2010, 00:03
par Ben314 » 05 Déc 2010, 00:03
O.K., mais ça utilise un théorème nettement plus fort (vu en terminale ?) que celui des valeurs intermédiaires qui est le seul utile avec la méthode f(a)-a>=0 et f(b)-b<=0 :
Un terminale est il sensé savoir que tout fonction continue sur un intervalle fermé borné atteint ses bornes ?
(tu en a besoin dans ta preuve pour justifier l'existence de ton 'a')
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Déc 2010, 10:41
par benekire2 » 05 Déc 2010, 10:41
Ben314 a écrit:O.K., mais ça utilise un théorème nettement plus fort (vu en terminale ?) que celui des valeurs intermédiaires qui est le seul utile avec la méthode f(a)-a>=0 et f(b)-b<=0 :
Un terminale est il sensé savoir que tout fonction continue sur un intervalle fermé borné atteint ses bornes ?
(tu en a besoin dans ta preuve pour justifier l'existence de ton 'a')
Oui je sais que je l'utilise , c'est pas un truc vu en Term , mais les profs nous le font ( en tout cas c'est notre cas ) admettre , et comme tout le monde trouve ça "graphiquement évident" ça gène pas trop, mais en effet ta preuve est nettement mieux comme toujours ... :zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Déc 2010, 10:48
par benekire2 » 05 Déc 2010, 10:48
Ben314 a écrit:tst sts sts, ce n'est pas aussi trivial que ça...
La suite Vn=|Un-L| est strictement décroissante et évidement minorée par 0 donc elle converge vers un certain lambda.
Mais pourquoi lambda est il forcément nul ?
Moi aussi j'avais pris cette méthode pour montrer la convergence de la suite vers son point fixe et ma première réaction fut d'utiliser Bolzano Weirestrass ... Mais en l'occurence on a plus simple :
V converge vers lR , ie après passage à la limite u converge vers l+L donc u converge, et si c'est bien le cas c'est vers son point fixe. Ainsi l=0 (sauf erreur)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2010, 10:55
par Ben314 » 05 Déc 2010, 10:55
benekire2 a écrit:...V converge vers lR , ie après passage à la limite u converge vers l+L...
Non : le fait que |Un-L| converge vers lambda n'implique pas que Un converge vers L+lambda...
Il me semble que le plus simple est de procéder par l'absurde en supposant que |Un-L|->lambda>0 puis d'utiliser la définition d'une limite avec par exemple epsilon=lambda/2>0...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Déc 2010, 11:17
par benekire2 » 05 Déc 2010, 11:17
Alors autant pour moi (zavais oublié le |.| ) :ptdr:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Déc 2010, 11:27
par benekire2 » 05 Déc 2010, 11:27
Sinon, ta méthode est encore mieux que la mienne ,

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2010, 11:56
par Ben314 » 05 Déc 2010, 11:56
La soluce qui me semble la plus "élémentaire" (mais pas vraiment la plus courte) (en blanc) :
Par l'absurde : si |Un-L|->T>0 alors, en prenant epsilon=T/2>0 dans la définition d'une limite, on sait qu'il existe N tel que, pour tout n>N, |Un-L| soit dans ]T/2,3T/2[ ce qui signifie que Un est dans un des deux intervalles I1=]L-3T/2,L-T/2[ ; I2=]L+T/2,L+3T/2[.
a) S'il existe deux termes succéssifs Up et U(p+1) qui sont dans le même intervalle Ik alors |Up-U(p+1)|p |Un-U(n+1)|p) sont dans l'intervale Ik donc que le signe de Un-L est constant et donc que Un tend vers L'=L-T (si k=1) ou vers L'=L+T (si k=2) et, comme U(n+1)=f(Un) on a f(L')=L' et donc |f(L)-f(L')|=L-L' avec L' différent de L : contradiction.
b) Si deux termes succéssifs ne sont jamais dans le même intervalle alors les U(2n)-L sont de signe constant (par exemple >0) donc U(2n) tend vers L+T. De même, U(2n+1) tend vers L-T.
Comme f(U(2n))=U(2n+1) on a f(L+T)=L-T donc |f(L+T)-f(L)|=T=|(L+T)-L| avec L et L+T distincts : contradiction.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Déc 2010, 11:59
par benekire2 » 05 Déc 2010, 11:59
Oui, moi c'est plus court , u est bornée donc une de ses sous suites converge vers l' et donc on arrive facilement a s'en sortir avec la décroissance de v ( deux lignes), pour ta méthode , on ne fait qu'utiliser le (faux ) argument que j'avais émis tout a l'heure en .. le rendant vrai . C'est plus long mais moins élémentaire , donc je préfère :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
telle que
qui est un peu plus rigolo.