Soient x,y,z trois longueurs des trois cotés dun triongle vérifies x+y+z=1
Montrez que : x²+y²+z² <1/2
EDIT : la politesse n'est pas en option.
Prouver l'inégalité
6 messages
- Page 1 sur 1
Salut,
 ,
,  et
et  sont solutions de l'équation suivante, avec
sont solutions de l'équation suivante, avec  le demi-périmètre,
le demi-périmètre,  le rayon du cercle inscrit et
le rayon du cercle inscrit et  circonscrit :
circonscrit :
a - 4prR = 0) (je te laisse montrer ça)
(je te laisse montrer ça)
D'après les relations de Viète :
 (1)
(1)
 (2)
(2)
 (3)
(3)
D'où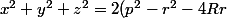)
Dans notre cas,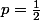 , d'où
, d'où 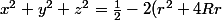 < \frac{1}{2})
Un résultat plus fort (en utilisant (3)) et ma relation montre que c'est la meilleure possible est :
D'après les relations de Viète :
D'où
Dans notre cas,
Un résultat plus fort (en utilisant (3)) et ma relation montre que c'est la meilleure possible est :
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
