Comment prouver que i=1

[neuneutrinos]

Hello world !
Je vais poser un petit problème auquel je me suis confronté.
Evidemment il y a une erreur ( et oui i et 1 c'est pas pareils :hum: )

L'exercice demandera la connaissance des nombres complexes et des logarithmes.







Jusque là rien de nouveau sous le soleil
et maintenant...











Ou est l'erreur de raisonnement ? :crunch:

[Monsieur23]

Aloha,

Malheureusement, le logarithme complexe est (beaucoup) plus compliqué que le logarithme réel… : http://www.wikiwand.com/fr/Logarithme_complexe

[neuneutrinos]

En fait, je connais la solution du problème.
Et on peut montrer l'erreur avec des outils niveau bac ( S )

L'idée est de faire un peu réflechir :)
(sinon je l'aurai mis dans la partie d'aide ;) )

[Sylviel]

Ben niveau bac S c'est pas compliqué : on ne peut pas écrire ln(i). :zen:

[neuneutrinos]

Ben niveau bac S c'est pas compliqué : on ne peut pas écrire ln(i). :zen:

Dans le plan complexe on ne peut pas non plus écrire ln(1) :lol3:
(que ce soit R -> C ou C -> C )
Et dire pourquoi ce n'est pas possible est démontrable avec des outils niveau bac.

Je pense que j'ai enoncé le problème de manière trop maladroit.

[vingtdieux]

Dans le plan complexe on ne peut pas non plus écrire ln(1) :lol3:
(que ce soit R -> C ou C -> C )
Et dire pourquoi ce n'est pas possible est démontrable avec des outils niveau bac.

Je pense que j'ai enoncé le problème de manière trop maladroit.

1= exp(i 2 k Pi)
Ln(1) = i 2 k Pi et c'est un pur imaginaire
Alors pour en revenir à la démo Ln(i^4) = 4 i Pi/2 = 2i Pi et c'est bien Ln(1) pour k=1
On pourrait mieux preciser les choses avec des modulo 2 Pi. Mais bon.....

[chan79]

Salut


mais le logarithme complexe est à prendre avec des pincettes, les formules uselles du logarithme réel n'étant pas forcément valables.

[Waax22951]

Je me suis toujours (enfin toujours, façon de dire..) posé une question: techniquement, on peut définir le logarithme puisque l'exponentielle est bijective sur et donc qu'elle admet une réciproque. Mais l'exponentielle complexe n'est pas bijective donc on ne peut pas définir le logarithme complexe comme cela.
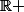
Cependant le logarithme népérien est aussi l'unique primitive de la fonction inverse sur s'annulant pour x=1. Existe-t-il une définition analogue au logarithme complexe ?
Je sais que la définition de la dérivation dans l'ensemble des nombres complexes est différente que dans les réels (une histoire de fonctions holomorphes dont je ne me suis jamais renseigné dessus), mais je pense qu'il existe une façon analogue pour définir les primitives, que je ne connais pas..

Bonne soirée et merci d'avance ! :lol3:

[Skullkid]

Salut, en gros, le logarithme complexe peut aussi se définir en tant que réciproque de l'exponentielle ou en tant que primitive de la fonction inverse. Le souci dans le premier cas c'est que tu dois restreindre l'ensemble de départ de l'exponentielle pour la rendre bijective. Dans le deuxième cas, le problème vient du fait qu'il y a plein de chemins différents pour aller d'un point A à un point B dans le plan complexe, alors que dans il n'y en a qu'un : la ligne droite. Du coup tu dois t'assurer que ta définition de l'intégrale ne dépend pas du chemin suivi, et malheureusement ça n'est pas le cas pour la fonction inverse sur (mais ça le devient si tu retires une demi-droite partant de 0).

[Waax22951]

Et est-ce qu'au final il existe une définition du logarithme comme réciproque de l'exponentielle qui coincide avec celle de la "primitive" de la fonction inverse ?

Merci d'avance ! :lol3:

[Skullkid]

Oui : la réciproque de l'exponentielle complexe restreinte à se trouve être l'unique primitive s'annulant en 1 de la fonction inverse restreinte à . C'est (à un chouïa près) ce qu'on appelle la détermination principale du logarithme complexe, et c'est en général à elle qu'on fait référence quand on parle "du" logarithme complexe.

[Waax22951]

D'accord, merci beaucoup ! :lol3:
D'ailleurs j'y pense: penses-tu qu'il est possible pour un élève de terminale qui a le temps d'apprendre les cours sur la dérivation dans le plan complexe ?
Si oui, où peut on trouver ces cours, s'il te plait ?

Merci d'avance et bonne soirée !

[vingtdieux]

On définit le logarithme du nombre complexe z par un nombre complexe w tel que e^w=z.
On aura w = log z = log |z| + i (Arg z+ 2 k Pi). Ainsi le logarithme d'un nombre complexe est une fonction à une infinité de valeurs. Celà fait penser à la relation qui existe entre les fonctions trigonométriques et leurs inverses. Arctg x a une infinité de valeurs.