Montrer que pour tout entier p>=3, il existe p nombres entiers
Egalité à prouver
10 messages
- Page 1 sur 1
Egalité à prouver
Voici un exercice qui - d'après moi - est très intéressant :
Montrer que pour tout entier p>=3, il existe p nombres entiers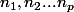 tels que :
tels que :

Montrer que pour tout entier p>=3, il existe p nombres entiers
salut
par récurrence
rang n : vrai
rang n+1 :
soit u un entier > nj pour un indice j <= n
soit k = (u*nj)/(u - nj) > 0 ca u > ni donc k entier naturel
alors
1/nj - 1/k = 1/u
dans la somme des 1/ni
1 <= i <= p,
on remplace l'entier nj par l'entier u
puis on pose
n_(p+1) = k
ainsi
la somme des 1/ni vaudra 1
car le + 1/n_(p+1) va faire que
1/u + 1/n_(p+1) = 1/u + 1/k = 1/nj
on va se retrouver avec notre somme qui, par récurrence, vaut 1.
par récurrence
rang n : vrai
rang n+1 :
soit u un entier > nj pour un indice j <= n
soit k = (u*nj)/(u - nj) > 0 ca u > ni donc k entier naturel
alors
1/nj - 1/k = 1/u
dans la somme des 1/ni
1 <= i <= p,
on remplace l'entier nj par l'entier u
puis on pose
n_(p+1) = k
ainsi
la somme des 1/ni vaudra 1
car le + 1/n_(p+1) va faire que
1/u + 1/n_(p+1) = 1/u + 1/k = 1/nj
on va se retrouver avec notre somme qui, par récurrence, vaut 1.
ok dans ce cas il faut juste choisir judicieusement mon entier u dans ma démo par récurrence ci-dessus.
Il faut u > ni pour tout i tel que
k = (u*nj)/(u - nj) soit un entier naturel > ni pour tout i pour un certain indice j.
On prend j tel que nj = max(ni)
alors
-nj² < 0
=>
-nj² < u*nj - u*nj
=>
nj(u - nj)
k = (u*nj)/(u-nj) > nj >= ni pour tout i
déja une condition de remplie
reste que k soit entier.
Et ca c'est évident, même en prenant u tres grand s'il le faut( de telle sorte que u différent de 2*nj sinon u = k...)
donc on aura k différent des a_i, u différent des a_i, par récurrence les a_i sont distincts deux à deux et comme dans ma démo précédente, on aura, si n_(p+1) = k,
somme des ni = 1
Il faut u > ni pour tout i tel que
k = (u*nj)/(u - nj) soit un entier naturel > ni pour tout i pour un certain indice j.
On prend j tel que nj = max(ni)
alors
-nj² < 0
=>
-nj² < u*nj - u*nj
=>
nj(u - nj)
k = (u*nj)/(u-nj) > nj >= ni pour tout i
déja une condition de remplie
reste que k soit entier.
Et ca c'est évident, même en prenant u tres grand s'il le faut( de telle sorte que u différent de 2*nj sinon u = k...)
donc on aura k différent des a_i, u différent des a_i, par récurrence les a_i sont distincts deux à deux et comme dans ma démo précédente, on aura, si n_(p+1) = k,
somme des ni = 1
J'ai aussi utilisé la réccurence :
Pour n=3, c'est trivial. On suppose que c'est juste pour n.
Il faut donc montrer que c'est juste pour n+1 il faut montrer que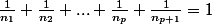
On sait que})
=>On conclut.
Belle solution namfoodle sheppen !!
lapras>> Je pense que t'as fait trop compliqué, non? ou c'est juste la mise en forme qui donne l'impression?
Pour n=3, c'est trivial. On suppose que c'est juste pour n.
Il faut donc montrer que c'est juste pour n+1 il faut montrer que
On sait que
=>On conclut.
Belle solution namfoodle sheppen !!
lapras>> Je pense que t'as fait trop compliqué, non? ou c'est juste la mise en forme qui donne l'impression?
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
