Bonjour à tous, je cherche une solution au problème suivant, merci d'avance à ceux qui voudront bien m'aider :
Soi les nombres de 1 à 21. Dans un tableau composé de sept colonnes et trois lignes, il faut ranger les nombres de 1 à 21 de sorte que la somme de chaque colonne fasse 33 et que la somme de chaque ligne fasse 77. On ne peut utiliser chaque nombre qu'une seule fois.
J'ai déjà trouvé plusieurs solutions possibles, par exemple :
1 21 19 13 5 6 12
15 10 3 16 8 18 7
17 2 11 4 20 9 14
ou bien
1 21 14 4 13 8 16
20 3 17 19 5 7 6
12 9 2 10 15 18 11
Je voudrais connaître toutes les solutions possibles : peut-on savoir le nombre de solutions possibles à ce problème (sachant aussi que l'ordre des colonnes importent peu) et j'aurais également besoin de connaître ces différentes solutions possibles.
Merci beaucoup d'avance merci !
Problème de type casse-tête carré magique
11 messages
- Page 1 sur 1
Re: Problème de type casse-tête carré magique
Salut,
Lorsque tu as une solution, si tu permute les 3 lignes (3!=6 façons de permuter) et les 7 colonnes (7!=5040 façons de permuter), ça reste une solution à ton problème.
Donc ça signifie qu'au total, il va y avoir un sacré paquet de solutions à ton problème mais ça signifie aussi qu'on peut se contenter de chercher les solutions avec un 1 en haut à gauche, la première ligne triée dans l'ordre croissant et la première colonne aussi (vu qu'en permutant les lignes et les colonnes on peut toujours se ramener à ce cas là).
EDIT : si je me suis pas gouré dans mon programme, je trouve 3062 solutions "primitives" (donc à multiplier par 6 et par 5040 pour les avoir toutes)
Lorsque tu as une solution, si tu permute les 3 lignes (3!=6 façons de permuter) et les 7 colonnes (7!=5040 façons de permuter), ça reste une solution à ton problème.
Donc ça signifie qu'au total, il va y avoir un sacré paquet de solutions à ton problème mais ça signifie aussi qu'on peut se contenter de chercher les solutions avec un 1 en haut à gauche, la première ligne triée dans l'ordre croissant et la première colonne aussi (vu qu'en permutant les lignes et les colonnes on peut toujours se ramener à ce cas là).
EDIT : si je me suis pas gouré dans mon programme, je trouve 3062 solutions "primitives" (donc à multiplier par 6 et par 5040 pour les avoir toutes)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème de type casse-tête carré magique
Salut Ben314 !
Merci pour ta réponse !
3062 solutions primitives ?? Ça me semble énorme ! C'est dingue, je pensais pas qu'il y en aurait autant.
J'ai continué de réfléchir au truc et là où j'en suis, je pense qu'en effet il faudrait un algorithme pour résoudre ce problème. Pour réduire au maximum le temps de recherche, j'ai répertorié toutes les combinaisons de trois nombres pouvant donner 33. Il y a cinquante combinaisons possibles. Je cherche donc à faire un algorithme pour répartir en 7 colonnes, ces 50 combinaisons possibles de colonnes, de façon à ce qu'aucun chiffre ne soit répété. Mais je n'ai aucune notion de code, seulement l'idée théorique du truc. J'ai tâtonné un peu avec Chatgpt mais ça ne fonctionne pas bien !
L'idée serait d'ajouter les combinaisons possibles par lignes dans un second temps.
Je ne me rends pas compte à quel point il est compliqué ou pas de faire ça.
Merci pour ta réponse !
3062 solutions primitives ?? Ça me semble énorme ! C'est dingue, je pensais pas qu'il y en aurait autant.
J'ai continué de réfléchir au truc et là où j'en suis, je pense qu'en effet il faudrait un algorithme pour résoudre ce problème. Pour réduire au maximum le temps de recherche, j'ai répertorié toutes les combinaisons de trois nombres pouvant donner 33. Il y a cinquante combinaisons possibles. Je cherche donc à faire un algorithme pour répartir en 7 colonnes, ces 50 combinaisons possibles de colonnes, de façon à ce qu'aucun chiffre ne soit répété. Mais je n'ai aucune notion de code, seulement l'idée théorique du truc. J'ai tâtonné un peu avec Chatgpt mais ça ne fonctionne pas bien !
L'idée serait d'ajouter les combinaisons possibles par lignes dans un second temps.
Je ne me rends pas compte à quel point il est compliqué ou pas de faire ça.
Re: Problème de type casse-tête carré magique
Dans une même colonne tu ne peut pas avoir deux nombres 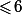 vu que 33-6-5>21.
vu que 33-6-5>21.
Donc les nombres 1,2,3,4,5,6 apparaissent dans 6 colonnes différentes, par exemple dans les 6 premières quitte à permuter les colonnes et, en conséquence, la 7em colonne ne contient que des nombres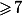 .
.
Avec un programme, et en commençant par la 7em colonne, on trouve rapidement qu'il n'y a que 84 répartitions possibles pour les colonnes.
Ensuite, j'y suis allé à la bourrin en regardant pour chacune des 84 répartitions toutes les façons de sommer le 1 de la première colonne avec un terme de chaque colonne (3^6=729 possibilités) et en ne retenant que les cas où la somme fait 77 (ça donne 1394 possibilités).
Et il ne reste plus qu'à faire la même chose, mais avec le deuxième terme de la première colonne et les deux termes non encore utilisés des autres colonnes (2^6=64 possibilités) pour chercher une deuxième somme égale à 77 :
Si tu sait pas utiliser le compilateur C de ton ordi., tu peut utiliser un interpréteur en ligne, par exemple là :
https://www.onlinegdb.com/online_c_compiler
Donc les nombres 1,2,3,4,5,6 apparaissent dans 6 colonnes différentes, par exemple dans les 6 premières quitte à permuter les colonnes et, en conséquence, la 7em colonne ne contient que des nombres
Avec un programme, et en commençant par la 7em colonne, on trouve rapidement qu'il n'y a que 84 répartitions possibles pour les colonnes.
Ensuite, j'y suis allé à la bourrin en regardant pour chacune des 84 répartitions toutes les façons de sommer le 1 de la première colonne avec un terme de chaque colonne (3^6=729 possibilités) et en ne retenant que les cas où la somme fait 77 (ça donne 1394 possibilités).
Et il ne reste plus qu'à faire la même chose, mais avec le deuxième terme de la première colonne et les deux termes non encore utilisés des autres colonnes (2^6=64 possibilités) pour chercher une deuxième somme égale à 77 :
- Code: Tout sélectionner
#include <stdio.h>
#include <stdlib.h>
int TB[3][7], OK[22];
int Nb;
void Affiche(void)
{ int x,y;
Nb++; printf("%4d : ",Nb);
for(y=0;y<7;y++)
{ for(x=0;x<3;x++) printf("%3d",TB[x][y]); printf(" ;"); }
printf("\n");
}
void Test2(void)
{ int l[7],i,Temp;
for(l[1]=1;l[1]<3;l[1]++) for(l[2]=1;l[2]<3;l[2]++) for(l[3]=1;l[3]<3;l[3]++)
for(l[4]=1;l[4]<3;l[4]++) for(l[5]=1;l[5]<3;l[5]++) for(l[6]=1;l[6]<3;l[6]++)
if(TB[1][0]+TB[l[1]][1]+TB[l[2]][2]+TB[l[3]][3]+TB[l[4]][4]+TB[l[5]][5]+TB[l[6]][6]==77)
{ for(i=1;i<7;i++) { Temp=TB[1][i]; TB[1][i]=TB[l[i]][i]; TB[l[i]][i]=Temp; }
Affiche();
for(i=1;i<7;i++) { Temp=TB[1][i]; TB[1][i]=TB[l[i]][i]; TB[l[i]][i]=Temp; }
} }
void Test1(void)
{ int l[7],i,Temp;
for(l[1]=0;l[1]<3;l[1]++) for(l[2]=0;l[2]<3;l[2]++) for(l[3]=0;l[3]<3;l[3]++)
for(l[4]=0;l[4]<3;l[4]++) for(l[5]=0;l[5]<3;l[5]++) for(l[6]=0;l[6]<3;l[6]++)
if(TB[0][0]+TB[l[1]][1]+TB[l[2]][2]+TB[l[3]][3]+TB[l[4]][4]+TB[l[5]][5]+TB[l[6]][6]==77)
{ for(i=1;i<7;i++) { Temp=TB[0][i]; TB[0][i]=TB[l[i]][i]; TB[l[i]][i]=Temp; }
Test2();
for(i=1;i<7;i++) { Temp=TB[0][i]; TB[0][i]=TB[l[i]][i]; TB[l[i]][i]=Temp; }
} }
void Recur(int k)
{ int min;
if(k<6)
{ if(k<4) min=11-k; else min=7;
for(TB[1][k]=min;(TB[2][k]=32-k-TB[1][k])>TB[1][k];TB[1][k]++)
if(OK[TB[1][k]]&&OK[TB[2][k]])
{ OK[TB[1][k]]=OK[TB[2][k]]=0;
Recur(k+1);
OK[TB[1][k]]=OK[TB[2][k]]=1;
} }
else Test1();
}
int main()
{ int i;
Nb=0; for(i=1;i<=21;i++) OK[i]=1;
for(i=0;i<6;i++) TB[0][i]=i+1;
for(TB[0][6]=7;TB[0][6]<=10;TB[0][6]++)
for(TB[1][6]=TB[0][6]+1;(TB[2][6]=33-TB[1][6]-TB[0][6])>TB[1][6];TB[1][6]++)
{ OK[TB[0][6]]=OK[TB[1][6]]=OK[TB[2][6]]=0;
Recur(0);
OK[TB[0][6]]=OK[TB[1][6]]=OK[TB[2][6]]=1;
}
}
Si tu sait pas utiliser le compilateur C de ton ordi., tu peut utiliser un interpréteur en ligne, par exemple là :
https://www.onlinegdb.com/online_c_compiler
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème de type casse-tête carré magique
Merci beaucoup !!
C'est super. Ca fait en effet énormément de possibilités... Du coup je serais intéressé par contre par les 84 répartitions possibles de colonnes. Est-ce que tu pourrais me les envoyer ou me fournir l'algorithme qui permet de les sortir ? Merci beaucoup !
C'est super. Ca fait en effet énormément de possibilités... Du coup je serais intéressé par contre par les 84 répartitions possibles de colonnes. Est-ce que tu pourrais me les envoyer ou me fournir l'algorithme qui permet de les sortir ? Merci beaucoup !
Re: Problème de type casse-tête carré magique
- Code: Tout sélectionner
1 : 1 11 21 ; 2 12 19 ; 3 14 16 ; 4 9 20 ; 5 13 15 ; 6 10 17 ; 7 8 18 ;
2 : 1 11 21 ; 2 14 17 ; 3 10 20 ; 4 13 16 ; 5 9 19 ; 6 12 15 ; 7 8 18 ;
3 : 1 11 21 ; 2 15 16 ; 3 10 20 ; 4 12 17 ; 5 9 19 ; 6 13 14 ; 7 8 18 ;
4 : 1 12 20 ; 2 10 21 ; 3 13 17 ; 4 14 15 ; 5 9 19 ; 6 11 16 ; 7 8 18 ;
5 : 1 12 20 ; 2 14 17 ; 3 9 21 ; 4 10 19 ; 5 13 15 ; 6 11 16 ; 7 8 18 ;
6 : 1 12 20 ; 2 15 16 ; 3 9 21 ; 4 10 19 ; 5 11 17 ; 6 13 14 ; 7 8 18 ;
7 : 1 13 19 ; 2 10 21 ; 3 14 16 ; 4 9 20 ; 5 11 17 ; 6 12 15 ; 7 8 18 ;
8 : 1 13 19 ; 2 11 20 ; 3 9 21 ; 4 14 15 ; 5 12 16 ; 6 10 17 ; 7 8 18 ;
9 : 1 15 17 ; 2 10 21 ; 3 11 19 ; 4 9 20 ; 5 12 16 ; 6 13 14 ; 7 8 18 ;
10 : 1 15 17 ; 2 11 20 ; 3 9 21 ; 4 10 19 ; 5 12 16 ; 6 13 14 ; 7 8 18 ;
11 : 1 11 21 ; 2 13 18 ; 3 10 20 ; 4 14 15 ; 5 12 16 ; 6 8 19 ; 7 9 17 ;
12 : 1 11 21 ; 2 13 18 ; 3 14 16 ; 4 10 19 ; 5 8 20 ; 6 12 15 ; 7 9 17 ;
13 : 1 11 21 ; 2 15 16 ; 3 12 18 ; 4 10 19 ; 5 8 20 ; 6 13 14 ; 7 9 17 ;
14 : 1 12 20 ; 2 10 21 ; 3 14 16 ; 4 11 18 ; 5 13 15 ; 6 8 19 ; 7 9 17 ;
15 : 1 12 20 ; 2 15 16 ; 3 11 19 ; 4 8 21 ; 5 10 18 ; 6 13 14 ; 7 9 17 ;
16 : 1 13 19 ; 2 10 21 ; 3 12 18 ; 4 14 15 ; 5 8 20 ; 6 11 16 ; 7 9 17 ;
17 : 1 13 19 ; 2 10 21 ; 3 14 16 ; 4 11 18 ; 5 8 20 ; 6 12 15 ; 7 9 17 ;
18 : 1 13 19 ; 2 11 20 ; 3 14 16 ; 4 8 21 ; 5 10 18 ; 6 12 15 ; 7 9 17 ;
19 : 1 14 18 ; 2 10 21 ; 3 11 19 ; 4 13 16 ; 5 8 20 ; 6 12 15 ; 7 9 17 ;
20 : 1 14 18 ; 2 12 19 ; 3 10 20 ; 4 8 21 ; 5 13 15 ; 6 11 16 ; 7 9 17 ;
21 : 1 11 21 ; 2 12 19 ; 3 13 17 ; 4 14 15 ; 5 8 20 ; 6 9 18 ; 7 10 16 ;
22 : 1 11 21 ; 2 14 17 ; 3 12 18 ; 4 9 20 ; 5 13 15 ; 6 8 19 ; 7 10 16 ;
23 : 1 12 20 ; 2 13 18 ; 3 9 21 ; 4 14 15 ; 5 11 17 ; 6 8 19 ; 7 10 16 ;
24 : 1 12 20 ; 2 14 17 ; 3 9 21 ; 4 11 18 ; 5 13 15 ; 6 8 19 ; 7 10 16 ;
25 : 1 12 20 ; 2 14 17 ; 3 11 19 ; 4 8 21 ; 5 13 15 ; 6 9 18 ; 7 10 16 ;
26 : 1 13 19 ; 2 14 17 ; 3 9 21 ; 4 11 18 ; 5 8 20 ; 6 12 15 ; 7 10 16 ;
27 : 1 14 18 ; 2 11 20 ; 3 9 21 ; 4 12 17 ; 5 13 15 ; 6 8 19 ; 7 10 16 ;
28 : 1 14 18 ; 2 11 20 ; 3 13 17 ; 4 8 21 ; 5 9 19 ; 6 12 15 ; 7 10 16 ;
29 : 1 15 17 ; 2 11 20 ; 3 12 18 ; 4 8 21 ; 5 9 19 ; 6 13 14 ; 7 10 16 ;
30 : 1 15 17 ; 2 12 19 ; 3 9 21 ; 4 11 18 ; 5 8 20 ; 6 13 14 ; 7 10 16 ;
31 : 1 12 20 ; 2 13 18 ; 3 14 16 ; 4 8 21 ; 5 9 19 ; 6 10 17 ; 7 11 15 ;
32 : 1 12 20 ; 2 14 17 ; 3 9 21 ; 4 13 16 ; 5 10 18 ; 6 8 19 ; 7 11 15 ;
33 : 1 13 19 ; 2 10 21 ; 3 14 16 ; 4 12 17 ; 5 8 20 ; 6 9 18 ; 7 11 15 ;
34 : 1 13 19 ; 2 14 17 ; 3 10 20 ; 4 8 21 ; 5 12 16 ; 6 9 18 ; 7 11 15 ;
35 : 1 14 18 ; 2 10 21 ; 3 13 17 ; 4 9 20 ; 5 12 16 ; 6 8 19 ; 7 11 15 ;
36 : 1 14 18 ; 2 12 19 ; 3 9 21 ; 4 13 16 ; 5 8 20 ; 6 10 17 ; 7 11 15 ;
37 : 1 11 21 ; 2 15 16 ; 3 13 17 ; 4 9 20 ; 5 10 18 ; 6 8 19 ; 7 12 14 ;
38 : 1 11 21 ; 2 15 16 ; 3 13 17 ; 4 10 19 ; 5 8 20 ; 6 9 18 ; 7 12 14 ;
39 : 1 13 19 ; 2 15 16 ; 3 9 21 ; 4 11 18 ; 5 8 20 ; 6 10 17 ; 7 12 14 ;
40 : 1 13 19 ; 2 15 16 ; 3 10 20 ; 4 8 21 ; 5 11 17 ; 6 9 18 ; 7 12 14 ;
41 : 1 15 17 ; 2 10 21 ; 3 11 19 ; 4 13 16 ; 5 8 20 ; 6 9 18 ; 7 12 14 ;
42 : 1 15 17 ; 2 11 20 ; 3 9 21 ; 4 13 16 ; 5 10 18 ; 6 8 19 ; 7 12 14 ;
43 : 1 15 17 ; 2 13 18 ; 3 9 21 ; 4 10 19 ; 5 8 20 ; 6 11 16 ; 7 12 14 ;
44 : 1 15 17 ; 2 13 18 ; 3 10 20 ; 4 8 21 ; 5 9 19 ; 6 11 16 ; 7 12 14 ;
45 : 1 11 21 ; 2 12 19 ; 3 13 17 ; 4 14 15 ; 5 10 18 ; 6 7 20 ; 8 9 16 ;
46 : 1 11 21 ; 2 14 17 ; 3 12 18 ; 4 10 19 ; 5 13 15 ; 6 7 20 ; 8 9 16 ;
47 : 1 12 20 ; 2 13 18 ; 3 11 19 ; 4 14 15 ; 5 7 21 ; 6 10 17 ; 8 9 16 ;
48 : 1 13 19 ; 2 10 21 ; 3 12 18 ; 4 14 15 ; 5 11 17 ; 6 7 20 ; 8 9 16 ;
49 : 1 13 19 ; 2 11 20 ; 3 12 18 ; 4 14 15 ; 5 7 21 ; 6 10 17 ; 8 9 16 ;
50 : 1 13 19 ; 2 14 17 ; 3 10 20 ; 4 11 18 ; 5 7 21 ; 6 12 15 ; 8 9 16 ;
51 : 1 14 18 ; 2 10 21 ; 3 11 19 ; 4 12 17 ; 5 13 15 ; 6 7 20 ; 8 9 16 ;
52 : 1 14 18 ; 2 11 20 ; 3 13 17 ; 4 10 19 ; 5 7 21 ; 6 12 15 ; 8 9 16 ;
53 : 1 15 17 ; 2 11 20 ; 3 12 18 ; 4 10 19 ; 5 7 21 ; 6 13 14 ; 8 9 16 ;
54 : 1 15 17 ; 2 12 19 ; 3 10 20 ; 4 11 18 ; 5 7 21 ; 6 13 14 ; 8 9 16 ;
55 : 1 11 21 ; 2 13 18 ; 3 14 16 ; 4 12 17 ; 5 9 19 ; 6 7 20 ; 8 10 15 ;
56 : 1 11 21 ; 2 14 17 ; 3 12 18 ; 4 13 16 ; 5 9 19 ; 6 7 20 ; 8 10 15 ;
57 : 1 12 20 ; 2 14 17 ; 3 11 19 ; 4 13 16 ; 5 7 21 ; 6 9 18 ; 8 10 15 ;
58 : 1 13 19 ; 2 11 20 ; 3 14 16 ; 4 12 17 ; 5 7 21 ; 6 9 18 ; 8 10 15 ;
59 : 1 13 19 ; 2 14 17 ; 3 9 21 ; 4 11 18 ; 5 12 16 ; 6 7 20 ; 8 10 15 ;
60 : 1 13 19 ; 2 14 17 ; 3 12 18 ; 4 9 20 ; 5 7 21 ; 6 11 16 ; 8 10 15 ;
61 : 1 14 18 ; 2 12 19 ; 3 9 21 ; 4 13 16 ; 5 11 17 ; 6 7 20 ; 8 10 15 ;
62 : 1 14 18 ; 2 12 19 ; 3 13 17 ; 4 9 20 ; 5 7 21 ; 6 11 16 ; 8 10 15 ;
63 : 1 12 20 ; 2 15 16 ; 3 13 17 ; 4 10 19 ; 5 7 21 ; 6 9 18 ; 8 11 14 ;
64 : 1 13 19 ; 2 15 16 ; 3 9 21 ; 4 12 17 ; 5 10 18 ; 6 7 20 ; 8 11 14 ;
65 : 1 13 19 ; 2 15 16 ; 3 10 20 ; 4 12 17 ; 5 7 21 ; 6 9 18 ; 8 11 14 ;
66 : 1 13 19 ; 2 15 16 ; 3 12 18 ; 4 9 20 ; 5 7 21 ; 6 10 17 ; 8 11 14 ;
67 : 1 15 17 ; 2 10 21 ; 3 12 18 ; 4 13 16 ; 5 9 19 ; 6 7 20 ; 8 11 14 ;
68 : 1 15 17 ; 2 12 19 ; 3 9 21 ; 4 13 16 ; 5 10 18 ; 6 7 20 ; 8 11 14 ;
69 : 1 15 17 ; 2 12 19 ; 3 10 20 ; 4 13 16 ; 5 7 21 ; 6 9 18 ; 8 11 14 ;
70 : 1 15 17 ; 2 13 18 ; 3 9 21 ; 4 10 19 ; 5 12 16 ; 6 7 20 ; 8 11 14 ;
71 : 1 14 18 ; 2 15 16 ; 3 9 21 ; 4 10 19 ; 5 11 17 ; 6 7 20 ; 8 12 13 ;
72 : 1 14 18 ; 2 15 16 ; 3 11 19 ; 4 9 20 ; 5 7 21 ; 6 10 17 ; 8 12 13 ;
73 : 1 15 17 ; 2 10 21 ; 3 14 16 ; 4 11 18 ; 5 9 19 ; 6 7 20 ; 8 12 13 ;
74 : 1 15 17 ; 2 11 20 ; 3 14 16 ; 4 10 19 ; 5 7 21 ; 6 9 18 ; 8 12 13 ;
75 : 1 12 20 ; 2 15 16 ; 3 13 17 ; 4 11 18 ; 5 7 21 ; 6 8 19 ; 9 10 14 ;
76 : 1 13 19 ; 2 15 16 ; 3 12 18 ; 4 8 21 ; 5 11 17 ; 6 7 20 ; 9 10 14 ;
77 : 1 15 17 ; 2 11 20 ; 3 12 18 ; 4 13 16 ; 5 7 21 ; 6 8 19 ; 9 10 14 ;
78 : 1 15 17 ; 2 13 18 ; 3 11 19 ; 4 8 21 ; 5 12 16 ; 6 7 20 ; 9 10 14 ;
79 : 1 14 18 ; 2 15 16 ; 3 10 20 ; 4 12 17 ; 5 7 21 ; 6 8 19 ; 9 11 13 ;
80 : 1 15 17 ; 2 12 19 ; 3 14 16 ; 4 8 21 ; 5 10 18 ; 6 7 20 ; 9 11 13 ;
81 : 1 14 18 ; 2 15 16 ; 3 13 17 ; 4 8 21 ; 5 9 19 ; 6 7 20 ; 10 11 12 ;
82 : 1 14 18 ; 2 15 16 ; 3 13 17 ; 4 9 20 ; 5 7 21 ; 6 8 19 ; 10 11 12 ;
83 : 1 15 17 ; 2 13 18 ; 3 14 16 ; 4 8 21 ; 5 9 19 ; 6 7 20 ; 10 11 12 ;
84 : 1 15 17 ; 2 13 18 ; 3 14 16 ; 4 9 20 ; 5 7 21 ; 6 8 19 ; 10 11 12 ;
Et le programme, c'est exactement le même sauf que dans la procédure "Recur", lorsque c'est fini (i.e. k=6) au lieu d'appeller "Test1" pour chercher les premières sommes faisant 77 (avec un terme par colonne), le programme appelle directement "Affiche" pour afficher le résultat.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème de type casse-tête carré magique
Je confirme les 3062 x 6 x 5040 solutions. Je trouve le même 3062 avec des méthodes différentes.
Par contre, je n'ai pas compris le '84'.
Par contre, je n'ai pas compris le '84'.
Re: Problème de type casse-tête carré magique
Le 84, c'est le nombre de façon de répartir les entiers de 1 à 21 en 7 paquets de trois entiers de façon à ce que la somme des trois entiers de chacun des 7 paquets fasse 33.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème de type casse-tête carré magique
Ok, c'était pourtant clair, mais je ne comprenais pas le gap entre 84 et ce 3062.
Pour passer de 84 à 3062, on "multiplie" par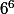 , mais on enlève les dispositions où les sommes horizontales ne donnent pas 77.
, mais on enlève les dispositions où les sommes horizontales ne donnent pas 77.
Pour passer de 84 à 3062, on "multiplie" par
Re: Problème de type casse-tête carré magique
You're welcome . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
