Oui, merci.
Le système se réécrit
\cos\alpha + R\sin\alpha&=a\end{aligned}\right.)
Une fois là, on peut confier la résolution à un système de calcul formel. J'utilise SageMath sui est libre et gratuit.
Je rentre les paramètres et variables du problème. Je prends
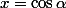
et
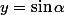
. Je résous le système linéaire en

et

, puis je résous
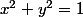
en

:
- Code: Tout sélectionner
a,b,c,d,R,x,y=var("a,b,c,d,R,x,y")
eq1 = R*x-d*y==R-b
eq2 = (c+d)*x+R*y==a
sol=solve([eq1,eq2],[x,y],solution_dict=True)[0]
eqR = sol[x]^2+sol[y]^2==1
sols=solve(eqR,R,solution_dict=True)
sols
Ça me sort des trucs atroces :
[{R: -1/12*(12*a*c - 12*c^2 - 24*c*d - 12*d^2 + (a^2 + b^2 - 2*a*c + c^2 - d^2)^2/b^2)*(-I*sqrt(3) + 1)/(18*(a^2 + b^2 - 2*a*c + c^2 - d^2)*(a*c - c^2 - 2*c*d - d^2)/b + (a^2 + b^2 - 2*a*c + c^2 - d^2)^3/b^3 + 54*(a^2*d^2 - c^2*d^2 - 2*c*d^3 - d^4 + (c^2 + 2*c*d + d^2)*b^2)/b + 18*sqrt(1/3*a^4 + 2/3*a^2*b^2 + 1/3*b^4 + 11/3*b^2*c^2 + 2/3*a*c^3 - 1/3*c^4 + 2/3*(2*a - c)*d^3 + 1/3*d^4 + 2/3*(3*a^2 + b^2 - 3*a*c)*d^2 - 2/3*(a^3 - 7*a*b^2)*c + 2/3*(2*a^3 + 2*a*b^2 + c^3 - (3*a^2 - 7*b^2)*c)*d)*(b^2*c - 2*(a - c)*d^2 + d^3 + (a^2 + b^2 - 2*a*c + c^2)*d)/b^2)^(1/3) - 1/12*(18*(a^2 + b^2 - 2*a*c + c^2 - d^2)*(a*c - c^2 - 2*c*d - d^2)/b + (a^2 + b^2 - 2*a*c + c^2 - d^2)^3/b^3 + 54*(a^2*d^2 - c^2*d^2 - 2*c*d^3 - d^4 + (c^2 + 2*c*d + d^2)*b^2)/b + 18*sqrt(1/3*a^4 + 2/3*a^2*b^2 + 1/3*b^4 + 11/3*b^2*c^2 + 2/3*a*c^3 - 1/3*c^4 + 2/3*(2*a - c)*d^3 + 1/3*d^4 + 2/3*(3*a^2 + b^2 - 3*a*c)*d^2 - 2/3*(a^3 - 7*a*b^2)*c + 2/3*(2*a^3 + 2*a*b^2 + c^3 - (3*a^2 - 7*b^2)*c)*d)*(b^2*c - 2*(a - c)*d^2 + d^3 + (a^2 + b^2 - 2*a*c + c^2)*d)/b^2)^(1/3)*(I*sqrt(3) + 1) + 1/6*(a^2 + b^2 - 2*a*c + c^2 - d^2)/b},
{R: -1/12*(12*a*c - 12*c^2 - 24*c*d - 12*d^2 + (a^2 + b^2 - 2*a*c + c^2 - d^2)^2/b^2)*(I*sqrt(3) + 1)/(18*(a^2 + b^2 - 2*a*c + c^2 - d^2)*(a*c - c^2 - 2*c*d - d^2)/b + (a^2 + b^2 - 2*a*c + c^2 - d^2)^3/b^3 + 54*(a^2*d^2 - c^2*d^2 - 2*c*d^3 - d^4 + (c^2 + 2*c*d + d^2)*b^2)/b + 18*sqrt(1/3*a^4 + 2/3*a^2*b^2 + 1/3*b^4 + 11/3*b^2*c^2 + 2/3*a*c^3 - 1/3*c^4 + 2/3*(2*a - c)*d^3 + 1/3*d^4 + 2/3*(3*a^2 + b^2 - 3*a*c)*d^2 - 2/3*(a^3 - 7*a*b^2)*c + 2/3*(2*a^3 + 2*a*b^2 + c^3 - (3*a^2 - 7*b^2)*c)*d)*(b^2*c - 2*(a - c)*d^2 + d^3 + (a^2 + b^2 - 2*a*c + c^2)*d)/b^2)^(1/3) - 1/12*(18*(a^2 + b^2 - 2*a*c + c^2 - d^2)*(a*c - c^2 - 2*c*d - d^2)/b + (a^2 + b^2 - 2*a*c + c^2 - d^2)^3/b^3 + 54*(a^2*d^2 - c^2*d^2 - 2*c*d^3 - d^4 + (c^2 + 2*c*d + d^2)*b^2)/b + 18*sqrt(1/3*a^4 + 2/3*a^2*b^2 + 1/3*b^4 + 11/3*b^2*c^2 + 2/3*a*c^3 - 1/3*c^4 + 2/3*(2*a - c)*d^3 + 1/3*d^4 + 2/3*(3*a^2 + b^2 - 3*a*c)*d^2 - 2/3*(a^3 - 7*a*b^2)*c + 2/3*(2*a^3 + 2*a*b^2 + c^3 - (3*a^2 - 7*b^2)*c)*d)*(b^2*c - 2*(a - c)*d^2 + d^3 + (a^2 + b^2 - 2*a*c + c^2)*d)/b^2)^(1/3)*(-I*sqrt(3) + 1) + 1/6*(a^2 + b^2 - 2*a*c + c^2 - d^2)/b},
{R: 1/6*(12*a*c - 12*c^2 - 24*c*d - 12*d^2 + (a^2 + b^2 - 2*a*c + c^2 - d^2)^2/b^2)/(18*(a^2 + b^2 - 2*a*c + c^2 - d^2)*(a*c - c^2 - 2*c*d - d^2)/b + (a^2 + b^2 - 2*a*c + c^2 - d^2)^3/b^3 + 54*(a^2*d^2 - c^2*d^2 - 2*c*d^3 - d^4 + (c^2 + 2*c*d + d^2)*b^2)/b + 18*sqrt(1/3*a^4 + 2/3*a^2*b^2 + 1/3*b^4 + 11/3*b^2*c^2 + 2/3*a*c^3 - 1/3*c^4 + 2/3*(2*a - c)*d^3 + 1/3*d^4 + 2/3*(3*a^2 + b^2 - 3*a*c)*d^2 - 2/3*(a^3 - 7*a*b^2)*c + 2/3*(2*a^3 + 2*a*b^2 + c^3 - (3*a^2 - 7*b^2)*c)*d)*(b^2*c - 2*(a - c)*d^2 + d^3 + (a^2 + b^2 - 2*a*c + c^2)*d)/b^2)^(1/3) + 1/6*(18*(a^2 + b^2 - 2*a*c + c^2 - d^2)*(a*c - c^2 - 2*c*d - d^2)/b + (a^2 + b^2 - 2*a*c + c^2 - d^2)^3/b^3 + 54*(a^2*d^2 - c^2*d^2 - 2*c*d^3 - d^4 + (c^2 + 2*c*d + d^2)*b^2)/b + 18*sqrt(1/3*a^4 + 2/3*a^2*b^2 + 1/3*b^4 + 11/3*b^2*c^2 + 2/3*a*c^3 - 1/3*c^4 + 2/3*(2*a - c)*d^3 + 1/3*d^4 + 2/3*(3*a^2 + b^2 - 3*a*c)*d^2 - 2/3*(a^3 - 7*a*b^2)*c + 2/3*(2*a^3 + 2*a*b^2 + c^3 - (3*a^2 - 7*b^2)*c)*d)*(b^2*c - 2*(a - c)*d^2 + d^3 + (a^2 + b^2 - 2*a*c + c^2)*d)/b^2)^(1/3) + 1/6*(a^2 + b^2 - 2*a*c + c^2 - d^2)/b}]
Il y a trois solutions, ce qui est normal parce qu'on aboutissait à une équation en

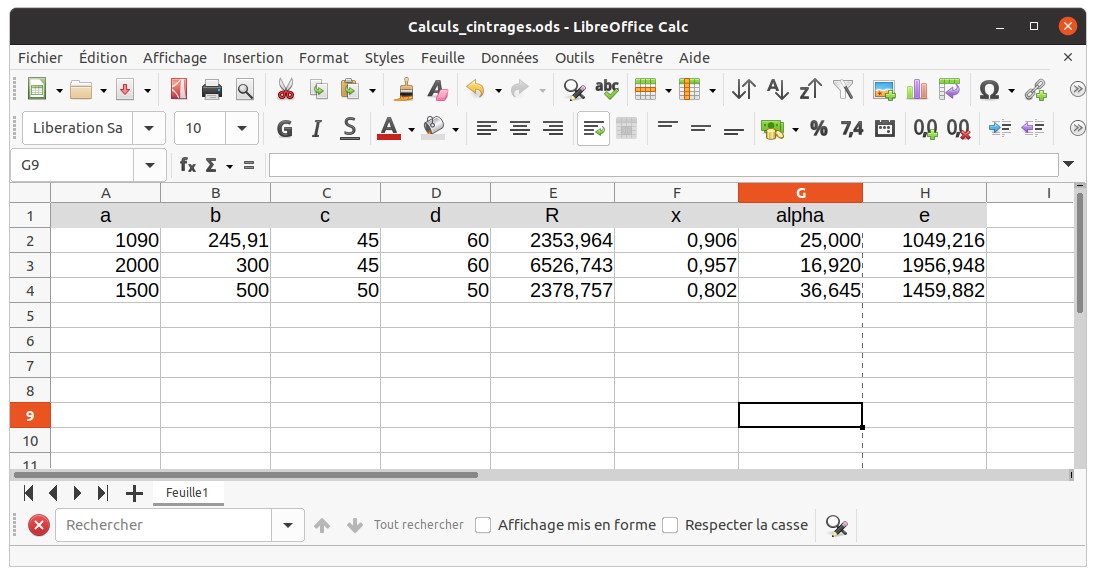
de degré 3. On remarque que la dernière est la seule solution réelle, on la choisit. Ensuite on évalue cette solution pour les données du graphique, on récupère l'angle

(donné en degrés, pratiquement 25°) et la cote manquante. Il y a bien sûr beaucoup de décimales, le calcul se fait en flottants.
- Code: Tout sélectionner
solR=sols[2][R]
donnees = a==1090, b==245.91, c==45, d==60
valR=solR.subs(donnees)
valR
2353.96372756431
- Code: Tout sélectionner
valx=sol[x].subs(donnees,R==valR)
alpha=arccos(valx)
alpha*180/pi.n()
25.0002639456978
- Code: Tout sélectionner
(a-c*valx).subs(donnees)
1049.21623719359