Bonjour à tous, et merci par avance à ceux qui viendront m'apporter leur aide.
dans le cadre de mon travail je suis confronté à une petite énigme mathématique un peu bloquante.
https://ibb.co/5h2GyHv
je suis à la recherche de l'angle en rouge, avec en données d'entrée les valeurs vertes.
Quelqu'un a une idée ?
Encore merci .
Cintrage arc
13 messages
- Page 1 sur 1
Re: Cintrage arc
Tu as C.e = 1000 et C.arc = 847.40
Je m'intéresse uniquement au demi-arc de gauche :
C.e2=500
C.arc2=423.70
C.e2-C.Arc2 =76.30
Et tu as F1=64.64
On a donc un triangle rectangle dont les côtés mesurent 76.30 et 64.64 pour les 2 premiers et ??? pour l'hypothénuse.
A partir de 76.30 et 64.64, on sait calculer l'angle demandé :
Tan(angle)= 64.64 /76.30
Angle= atan(64.64/6.30) = 0.7028
Attention, les outils standard donnent les angles en radians, et toi, tu veux un angle en degrés.
Angle = (180/PI ) * atan(64.64/6.30) =40.2706764 °
On retrouve bien le nombre indiqué sur la figure.
Je m'intéresse uniquement au demi-arc de gauche :
C.e2=500
C.arc2=423.70
C.e2-C.Arc2 =76.30
Et tu as F1=64.64
On a donc un triangle rectangle dont les côtés mesurent 76.30 et 64.64 pour les 2 premiers et ??? pour l'hypothénuse.
A partir de 76.30 et 64.64, on sait calculer l'angle demandé :
Tan(angle)= 64.64 /76.30
Angle= atan(64.64/6.30) = 0.7028
Attention, les outils standard donnent les angles en radians, et toi, tu veux un angle en degrés.
Angle = (180/PI ) * atan(64.64/6.30) =40.2706764 °
On retrouve bien le nombre indiqué sur la figure.
Re: Cintrage arc
lyceen95 a écrit:Tu as C.e = 1000 et C.arc = 847.40
Je m'intéresse uniquement au demi-arc de gauche :
C.e2=500
C.arc2=423.70
C.e2-C.Arc2 =76.30
Et tu as F1=64.64
On a donc un triangle rectangle dont les côtés mesurent 76.30 et 64.64 pour les 2 premiers et ??? pour l'hypothénuse.
A partir de 76.30 et 64.64, on sait calculer l'angle demandé :
Tan(angle)= 64.64 /76.30
Angle= atan(64.64/6.30) = 0.7028
Attention, les outils standard donnent les angles en radians, et toi, tu veux un angle en degrés.
Angle = (180/PI ) * atan(64.64/6.30) =40.2706764 °
On retrouve bien le nombre indiqué sur la figure.
Bonjour et merci pour ta réponse.
Les données d'entrées sont
C.e + Pied droit + F.e
ta méthode serait utilisable si nous définissons dans un premier temps le "C.arc"
dans mon image j'ai utilisé graphiquement ces données d'entrée pour résoudre mon problème mais je n'ai pas initialement les données que tu utilises pour la résolution (C.arc par exemple)
les seules valeurs connues sont celles en vert.
Re: Cintrage arc
Ah !!!
Je pense qu'il manque alors une information
On a la hauteur F.e=220.
Mais on ne peut rien en faire.
Le seul cas où on peut utiliser cette information, c'est si on nous dit : l'arc plus ou moins arrondi est un arc de cercle (ou au moins, si on nous donne sa nature, parabole, hyperbole...)
Si l'arc est quelconque, on ne peut pas exploiter le 220, et on ne peut pas conclure.
Si on nous dit que c'est un arc de cercle, on doit pouvoir s'en sortir, mais je n'ai pas le courage de chercher.
Je pense qu'il manque alors une information
On a la hauteur F.e=220.
Mais on ne peut rien en faire.
Le seul cas où on peut utiliser cette information, c'est si on nous dit : l'arc plus ou moins arrondi est un arc de cercle (ou au moins, si on nous donne sa nature, parabole, hyperbole...)
Si l'arc est quelconque, on ne peut pas exploiter le 220, et on ne peut pas conclure.
Si on nous dit que c'est un arc de cercle, on doit pouvoir s'en sortir, mais je n'ai pas le courage de chercher.
Re: Cintrage arc
lyceen95 a écrit:Ah !!!
Je pense qu'il manque alors une information
On a la hauteur F.e=220.
Mais on ne peut rien en faire.
Le seul cas où on peut utiliser cette information, c'est si on nous dit : l'arc plus ou moins arrondi est un arc de cercle (ou au moins, si on nous donne sa nature, parabole, hyperbole...)
Si l'arc est quelconque, on ne peut pas exploiter le 220, et on ne peut pas conclure.
Si on nous dit que c'est un arc de cercle, on doit pouvoir s'en sortir, mais je n'ai pas le courage de chercher.
Il s'agit effectivement d'un arc de cercle de rayon R (=655.45 sur l'exemple --> cote inconnue)
le pied droit et cet arc de cercle sont tangents.
Re: Cintrage arc
Bonjour,
le rayon de l'arc de cercle est quand même connu, sinon je ne vois pas comment tu le traces
le rayon de l'arc de cercle est quand même connu, sinon je ne vois pas comment tu le traces
Re: Cintrage arc
Non, le rayon peut parfaitement être une des inconnues.
On va donner des noms aux différents points.
A le point tout à gauche.
B le point à 100 mm de A, où l'arc de cercle commence.
H le point tout en haut du dessin.
O le point au milieu de la droite horizontale partant de A.
C le centre du cercle.
Et l'angle cherché, nommons le t
Et R=le rayon du cercle.
O est le centre de notre repère.
Donc O(0,0)
A(-500,0)
B(-500+100cos(t), 100sin(t) )
H(0,220)
C(0,220-R)
On a quelques équations :
L'angle HCB vaut t
Donc le vecteur CB est (-R sin(t), R cos(t) )
Donc -500+100 cos(t) = -R sin(t) et 100 sin(t)-220+R = R cos(t)
On a 2 équations, et 2 inconnues t et R ... on est bien parti.
Qui veut continuer ?
J'ai mis les valeurs numériques (500,100,220) ... donc on connaît d'avance la réponse. En vrai, il faut refaire en mettant (500,100, x) , voire (y,z,x)
On va donner des noms aux différents points.
A le point tout à gauche.
B le point à 100 mm de A, où l'arc de cercle commence.
H le point tout en haut du dessin.
O le point au milieu de la droite horizontale partant de A.
C le centre du cercle.
Et l'angle cherché, nommons le t
Et R=le rayon du cercle.
O est le centre de notre repère.
Donc O(0,0)
A(-500,0)
B(-500+100cos(t), 100sin(t) )
H(0,220)
C(0,220-R)
On a quelques équations :
L'angle HCB vaut t
Donc le vecteur CB est (-R sin(t), R cos(t) )
Donc -500+100 cos(t) = -R sin(t) et 100 sin(t)-220+R = R cos(t)
On a 2 équations, et 2 inconnues t et R ... on est bien parti.
Qui veut continuer ?
J'ai mis les valeurs numériques (500,100,220) ... donc on connaît d'avance la réponse. En vrai, il faut refaire en mettant (500,100, x) , voire (y,z,x)
Re: Cintrage arc
lyceen95 a écrit:Non, le rayon peut parfaitement être une des inconnues.
d'accord avec toi pour pouvoir faire la démo dans le cas général mais pour le dessin il faut bien fixer le rayon, non?
Re: Cintrage arc
Pisigma a écrit:lyceen95 a écrit:Non, le rayon peut parfaitement être une des inconnues.
d'accord avec toi pour pouvoir faire la démo dans le cas général mais pour le dessin il faut bien fixer le rayon, non?
Bonjour,
Non le fait que l'arc et le pied droit soient tangents, les 3 autres données te forment forcement une géométrie figée.
lyceen95 a écrit:Non, le rayon peut parfaitement être une des inconnues.
On va donner des noms aux différents points.
A le point tout à gauche.
B le point à 100 mm de A, où l'arc de cercle commence.
H le point tout en haut du dessin.
O le point au milieu de la droite horizontale partant de A.
C le centre du cercle.
Et l'angle cherché, nommons le t
Et R=le rayon du cercle.
O est le centre de notre repère.
Donc O(0,0)
A(-500,0)
B(-500+100cos(t), 100sin(t) )
H(0,220)
C(0,220-R)
On a quelques équations :
L'angle HCB vaut t
Donc le vecteur CB est (-R sin(t), R cos(t) )
Donc -500+100 cos(t) = -R sin(t) et 100 sin(t)-220+R = R cos(t)
On a 2 équations, et 2 inconnues t et R ... on est bien parti.
Qui veut continuer ?
J'ai mis les valeurs numériques (500,100,220) ... donc on connaît d'avance la réponse. En vrai, il faut refaire en mettant (500,100, x) , voire (y,z,x)
Bonjour,
Merci pour cette réflexion.
ça me parait parfaitement logique
J'ai un peu de mal à résoudre l'équation. Je vais essayer de persévérer un peu.
Si quelqu'un passe par là, pour qui c'est une broutille, je ne suis pas contre une nouvelle aide.
Encore merci
Re: Cintrage arc
J'ai continué les calculs de mon côté samedi, mais je sais que je m'étais planté quelque part, et je n'ai pas eu le courage de refaire.
Je recopie quand même.
J'arrivais à ça :
100 cos(t) +R sin(t) = 500
100 sin(t) - R cos(t) = 220-R
Ici, on a une forme très pratique à exploiter.
On introduit un nombre k= racine ( 100²+R²)
et un angle a tel que sin (a)= 100/k et cos a = R/k ou encore tan(a)= 100/R
Et on utilise les formules classiques cos(u+v)= .. et sin(u+v)=..
ça donne :
k sin(a+t)=500
k cos(a+t)=R-220
Et donc tan(a+t)= 500/(R-220)
Je viens de détecter une de mes erreurs... Donc ceci devrait être bon.
Une formule 'mathématique' qui va donner R et t ... je ne suis pas sûr que ça aboutisse.
Mais par programmation, par dichotomie, ça devrait aboutir : on fait varier R, on calcule a et t par les formules ici :
a = atan(100/R)
t = atan(500/(R-220))-a
et on vérifie si 100 cos(t) +R sin(t) donne 500
Tant que 100 cos(t) +R sin(t) est inférieur à 500 on augmente R , et inversement, si 100 cos(t)
+R sin(t) , on diminue R. ( ou bien, c'est exactement l'inverse ... je te laisse vérifier)
Pas sûr de tous les calculs, mais la trame est là.
Je recopie quand même.
J'arrivais à ça :
100 cos(t) +R sin(t) = 500
100 sin(t) - R cos(t) = 220-R
Ici, on a une forme très pratique à exploiter.
On introduit un nombre k= racine ( 100²+R²)
et un angle a tel que sin (a)= 100/k et cos a = R/k ou encore tan(a)= 100/R
Et on utilise les formules classiques cos(u+v)= .. et sin(u+v)=..
ça donne :
k sin(a+t)=500
k cos(a+t)=R-220
Et donc tan(a+t)= 500/(R-220)
Je viens de détecter une de mes erreurs... Donc ceci devrait être bon.
Une formule 'mathématique' qui va donner R et t ... je ne suis pas sûr que ça aboutisse.
Mais par programmation, par dichotomie, ça devrait aboutir : on fait varier R, on calcule a et t par les formules ici :
a = atan(100/R)
t = atan(500/(R-220))-a
et on vérifie si 100 cos(t) +R sin(t) donne 500
Tant que 100 cos(t) +R sin(t) est inférieur à 500 on augmente R , et inversement, si 100 cos(t)
+R sin(t) , on diminue R. ( ou bien, c'est exactement l'inverse ... je te laisse vérifier)
Pas sûr de tous les calculs, mais la trame est là.
Re: Cintrage arc
autre approche en repartant de
 +R\, sin(t) = 500)
 - R\, cos(t) = 220-R)
en réécrivant les 2 équations sous la forme
=500-100\, cos(t)(1))
)=220 -100\, sin(t)(2))
}{(2)}) avec
avec )
}{1-cos(t)}=\dfrac{50-10\, cos(t)}{22-10\, sin(t)})
en développant et regroupant des termes on obtient
+22\, sin(t)-60=0\,(3))
posons=x\,(4))
(3) devient}{1+x^2}+ \dfrac{44\,x}{1+x^2}-60=0)
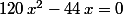 soit
soit =0) soit
soit  (à rejeter d'après (*)) ou
(à rejeter d'après (*)) ou 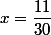
(4) donne=\dfrac{11}{30}, \dfrac{t}{2}=20.136\textdegree\,\,[k\pi]\, t=40.272\textdegree(5))
(5) dans (1) donne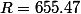
sauf erreur de recopie!!
en réécrivant les 2 équations sous la forme
en développant et regroupant des termes on obtient
posons
(3) devient
(4) donne
(5) dans (1) donne
sauf erreur de recopie!!
Re: Cintrage arc
Salut,
Pour simplifier, je prend ça comme notations :
D = pied droit = 100
2L = C.e = 1000 (donc L=500)
H = F.e = 220
En utilisant deux fois Pythagore pour calculer le carré de la distance du centre de l'arc à une extrémité de la tige, on obtient :
(H-R)^2 + L^2 = R^2 + D^2
Qui permet d'obtenir la valeur du rayon R de l'arc :
R = (L^2 +H^2 - D^2) / (2H)
Ensuite un peu de trio. donne rapidement
cos (theta) = (DH-DR+LR) / (D^2+R^2)
sin (theta) = (DL-HR+R^2) / (D^2+R^2)
Pour simplifier, je prend ça comme notations :
D = pied droit = 100
2L = C.e = 1000 (donc L=500)
H = F.e = 220
En utilisant deux fois Pythagore pour calculer le carré de la distance du centre de l'arc à une extrémité de la tige, on obtient :
(H-R)^2 + L^2 = R^2 + D^2
Qui permet d'obtenir la valeur du rayon R de l'arc :
R = (L^2 +H^2 - D^2) / (2H)
Ensuite un peu de trio. donne rapidement
cos (theta) = (DH-DR+LR) / (D^2+R^2)
sin (theta) = (DL-HR+R^2) / (D^2+R^2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cintrage arc
Ben314 a écrit:Salut,
Pour simplifier, je prend ça comme notations :
D = pied droit = 100
2L = C.e = 1000 (donc L=500)
H = F.e = 220
En utilisant deux fois Pythagore pour calculer le carré de la distance du centre de l'arc à une extrémité de la tige, on obtient :
(H-R)^2 + L^2 = R^2 + D^2
Qui permet d'obtenir la valeur du rayon R de l'arc :
R = (L^2 +H^2 - D^2) / (2H)
Ensuite un peu de trio. donne rapidement
cos (theta) = (DH-DR+LR) / (D^2+R^2)
sin (theta) = (DL-HR+R^2) / (D^2+R^2)
Bonjour et merci à tous et particulièrement à Ben314 pour cette réponse claire et efficace.
C'est la solution que je recherchais.
Je vais essayer de comprendre un peu tout ça mais en tout cas, ça fonctionne !!
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
