Probabilités liées et indépendantes encore n°2
92 messages
- Page 3 sur 5 - 1, 2, 3, 4, 5
Re: des probas sans compter
[………………………...
Modifié en dernier par beagle le 14 Mai 2019, 16:08, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: des probas sans compter
GaBuZoMeu a écrit:C'est une belle histoire, mais ce n'est pas des mathématiques.
ok, j'ai retiré ce qui n'était pas mathématique.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: des probas sans compter
……………………………………………...
Modifié en dernier par beagle le 14 Mai 2019, 16:55, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: des probas sans compter
Non Beagle , on ne peut pas retirer un sujet ayant suscité des réponses , après tu peux retirer le reste .
Imod
Imod
Re: des probas sans compter
Imod a écrit:Non Beagle , on ne peut pas retirer un sujet ayant suscité des réponses , après tu peux retirer le reste .
Imod
mes messages sont à durée de vie limitée, ils meurent passés un certains temps...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: des probas sans compter
Je ne parle pas de tes messages mais du problème que tu as proposé et qui a suscité quelques réponses . tu peux claquer la porte si le problème ne t'intéresse plus mais tu n'es pas seul dans l'histoire .
Imod
PS : personnellement je ne connais même pas la question originale
Imod
PS : personnellement je ne connais même pas la question originale

Re: des probas sans compter
[.................................
Modifié en dernier par beagle le 14 Mai 2019, 17:45, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: des probas sans compter
J'ai lu , tu peux virer ce message et au passage remettre le problème initial , c'est la moindre des choses , non ?
Imod
Imod
Re: des probas sans compter
Imod a écrit:J'ai lu , tu peux virer ce message et au passage remettre le problème initial , c'est la moindre des choses , non ?
Imod
ce que je ne supportais plus sur tes fils de discussion, c'est ton attitude professorale.
attitude de beaucoup d'ailleurs en ce moment sur le forum…
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: des probas sans compter
hi GaBuZoMeu,
je pense comprendre les affirmations, mais je voudrais être sûr de pas délirer surtout sur les "Donc"
> Le nombre d'éléments de f^{-1}(u) est le même pour tous les u de U (1e affirmation)
De ce que j'ai compris:
1ere affirmation:
u de U est de la forme
[1,4,5,6,7,8,10,11
0 0 0 0 1 1 1 0]
la premiere ligne donnant le num du tour et la deuxieme ligne qui a eu le coeur
f^-1(u) permet de retrouver le nombre d'elem de C tq on ait obtenu ce u.
donc qqch comme
(24)*8 * //tour 1
(23*22) //tour 2
(21*20) //tour 3
19*7 //tour 4
18*6 //tour 5
17*5 //tour 6
...
2*1 //tour 16
...
la 1ere affirmation est ok(si je l'ai bien comprise..) vu que on "fixe" le coeur 8 fois, et on "complete" avec le reste
le Donc se sert du fait que f^{-1}(V) = A et f^{-1}(U) = C
la seule manière que j'ai de justifier l'égalité est de l'ordre de
card(A) = card(f^{-1}(V)) = kcard(V) et card(C) = kcard(U)
et les k se simplifient
pour la deuxieme affirmation:
pour les 8 coeurs placés, on associe respectivement 16,15,14...,9 (les noirs) puis on complete par
8,8 //carreaux à gauche, noirs à droite ou le contraire..
7,7
le deuxieme Donc j'ai plus de mal...
Si on part du principe que B est inclus dans C (??)
f^{-1}(U) inter B = C inter B = B et
f^{-1}(V) inter B = A inter B
mais comment faire intervenir les cardinaux?
je pense comprendre les affirmations, mais je voudrais être sûr de pas délirer surtout sur les "Donc"
> Le nombre d'éléments de f^{-1}(u) est le même pour tous les u de U (1e affirmation)
De ce que j'ai compris:
1ere affirmation:
u de U est de la forme
[1,4,5,6,7,8,10,11
0 0 0 0 1 1 1 0]
la premiere ligne donnant le num du tour et la deuxieme ligne qui a eu le coeur
f^-1(u) permet de retrouver le nombre d'elem de C tq on ait obtenu ce u.
donc qqch comme
(24)*8 * //tour 1
(23*22) //tour 2
(21*20) //tour 3
19*7 //tour 4
18*6 //tour 5
17*5 //tour 6
...
2*1 //tour 16
...
la 1ere affirmation est ok(si je l'ai bien comprise..) vu que on "fixe" le coeur 8 fois, et on "complete" avec le reste
le Donc se sert du fait que f^{-1}(V) = A et f^{-1}(U) = C
la seule manière que j'ai de justifier l'égalité est de l'ordre de
card(A) = card(f^{-1}(V)) = kcard(V) et card(C) = kcard(U)
et les k se simplifient
pour la deuxieme affirmation:
pour les 8 coeurs placés, on associe respectivement 16,15,14...,9 (les noirs) puis on complete par
8,8 //carreaux à gauche, noirs à droite ou le contraire..
7,7
le deuxieme Donc j'ai plus de mal...
Si on part du principe que B est inclus dans C (??)
f^{-1}(U) inter B = C inter B = B et
f^{-1}(V) inter B = A inter B
mais comment faire intervenir les cardinaux?
la vie est une fête 
Re: des probas sans le dire mais en musique
Je vois que tu te mets à compter. Attention, c'est interdit.
Je n'ai pas justifié mes affirmations. Mais la justification consiste, étant donné deux éléments et
et 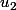 de
de  , en la construction d'une bijection de
, en la construction d'une bijection de ) sur
sur ) qui envoie
qui envoie \cap B) sur
sur \cap B) . La construction de cette bijection est un peu casse-pieds à décrire formellement, mais l'idée de construction est assez évidente : en gros, on fait une permutation des tours de distribution qui envoie un tour de distribution avec coeur sur un tour de distribution avec coeur, et à l'intérieur d'un tour de distribution avec coeur on échange les cartes de Yves et Pierre quand il le faut.
. La construction de cette bijection est un peu casse-pieds à décrire formellement, mais l'idée de construction est assez évidente : en gros, on fait une permutation des tours de distribution qui envoie un tour de distribution avec coeur sur un tour de distribution avec coeur, et à l'intérieur d'un tour de distribution avec coeur on échange les cartes de Yves et Pierre quand il le faut.
Une fois que ceci est fait, on a démontré que tous les) ont même nombre d'éléments, appelons-le
ont même nombre d'éléments, appelons-le  , et que tous les
, et que tous les \cap B) ont me nombre d'éléments, appelons-le
ont me nombre d'éléments, appelons-le  .
.
On a donc :
 = \gamma\times \sharp V)
 = \gamma\times \sharp U)
 =\sharp(f^{-1}(V)\cap B) = \beta\times \sharp V)
\cap B) = \beta\times \sharp U)
et il suit que
= \sharp (A\cap B)/ \sharp B=\sharp V/\sharp U=\sharp A/\sharp C= P(A\mid C) = P_3)
Tu n'en es pas convaincu ? Tu n'es pas convaincu que demander qu'il n'y ait jamais deux cartes de même couleur dans un tour de distribution, c'est plus fort que de demander qu'il n'y ait jamais deux coeurs dans un tour de distribution ???
Je n'ai pas justifié mes affirmations. Mais la justification consiste, étant donné deux éléments
Une fois que ceci est fait, on a démontré que tous les
On a donc :
et il suit que
Si on part du principe que B est inclus dans C (??)
Tu n'en es pas convaincu ? Tu n'es pas convaincu que demander qu'il n'y ait jamais deux cartes de même couleur dans un tour de distribution, c'est plus fort que de demander qu'il n'y ait jamais deux coeurs dans un tour de distribution ???
Re: des probas sans le dire mais en musique
Tu n'en es pas convaincu ?
jetais déjà pas sûr de ma notation ensembliste
mais c'est clair now, thx
la vie est une fête 
Re: Probabilités liées et indépendantes encore n°2
Beagle a écrit:On prend comme proba qu'"Yves" reçoive les 8 cartes cœurs,
la multiplication proba avoir la premiere, fois proba avoir la seconde sachant qu'on a la première, ...fois proba d'avoir la huitième sachant qu'on a les 7 premieres.
On s'intéressera donc à la proba d'avoir la (k+1) carte cœur sachant qu'on a déjà les k premières.
On part pour première carte cœur d'une proba à 1/2 dans les 4 cas de figure
-Pour 2 et 3:
On montre alors facilement que pour les questions 2 et 3, la proba reste à 1/2 tout le temps,
c'est la situation d'indépendance p((k+1)/k) = p(k+1)
qui est d'ailleurs vraie pour tout ensemble de cartes cœur par rapport à un autre ensemble disjoint, connaitre la réalisation de l'un ne joue pas sur la proba de l'autre groupe.
P2 = P3
-Pour la 1:
on montre facilement que la proba k+1 est inférieure à la proba k
donc on multipliera 7 fois du plus petit que 1/2 au 1/2 initial
P1 est la plus basse des 4 probas
-pour la 4:
on montre facilement la proba de k+1 est au minimum à 1/2 et au maximum à plus de 1/2, en moyenne plus que 1/2
On va donc multiplier 7 fois du plus que 1/2 au 1/2 initial
P4 est la plus élevée des probas
Moi, je veux bien, Beagle. Je demande simplement à voir une explicitation des "On montre facilement que". C'est un réflexe d'arbitre pour les publications : le diable dans les textes mathématiques se cache très souvent dans les "on montre facilement que...", "il est clair que ..." etc.
Le résultat final ne fait pas de doute. Le problème est dans le fait que les arguments soient mathématiquement convaincants ou pas.
Re: Probabilités liées et indépendantes encore n°2
"Moi, je veux bien, Beagle. Je demande simplement à voir une explicitation des "On montre facilement que". C'est un réflexe d'arbitre pour les publications : le diable dans les textes mathématiques se cache très souvent dans les "on montre facilement que...", "il est clair que ..." etc.
Le résultat final ne fait pas de doute. Le problème est dans le fait que les arguments soient mathématiquement convaincants ou pas."
la démonstration était dans le fil de discussion,
tu l'avais lu????????
Le résultat final ne fait pas de doute. Le problème est dans le fait que les arguments soient mathématiquement convaincants ou pas."
la démonstration était dans le fil de discussion,
tu l'avais lu????????
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités liées et indépendantes encore n°2
Je te fais le difficile cas numéro 3
on note 2n le nombre de cartes
proba ((k+1)/ k)= (n-k)/ (2n-2k)
proba avoir la k+1 iem carte sachant qu'on a déjà les k premieres est 1/2
et c'est vrai pour un ensemble A de cartes cœurs et un ensemble B de cartes coeur, ensembles disjoints
a= Yves reçoit les cartesA
b = Yves reçoit les cartes B
P(a/b) = P(a)
c'est indépendance,
then end
on note 2n le nombre de cartes
proba ((k+1)/ k)= (n-k)/ (2n-2k)
proba avoir la k+1 iem carte sachant qu'on a déjà les k premieres est 1/2
et c'est vrai pour un ensemble A de cartes cœurs et un ensemble B de cartes coeur, ensembles disjoints
a= Yves reçoit les cartesA
b = Yves reçoit les cartes B
P(a/b) = P(a)
c'est indépendance,
then end
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités liées et indépendantes encore n°2
Quant à dire que l'on ne compte pas lorsque l'on utilise l'inclusion d'ensembles finis, et des surjections, bijections,
ben disons que …
https://www.youtube.com/watch?v=CTE08SS8fNk
ben disons que …
https://www.youtube.com/watch?v=CTE08SS8fNk
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités liées et indépendantes encore n°2
beagle a écrit:Je te fais le difficile cas numéro 3
on note 2n le nombre de cartes
proba ((k+1)/ k)= (n-k)/ (2n-2k)
proba avoir la k+1 iem carte sachant qu'on a déjà les k premieres est 1/2
Là tu écris une affirmation. Je demande un argument. En particulier, que tu explicites comment tu utilises les hypothèses du 3. Pourquoi y a-t-il, parmi les distributions satisfaisant à la condition 3 et telles que Yves a les k premières cartes de coeur, autant de distributions pour lesquelles Yves a la k+1 - ème que de distributions pour lesquelles c'est Pierre qui a la k+1-ème.
"C'est évident" n'est pas une réponse. Si tu veux donner un argument d'indépendance, j'attends que tu démontres l'indépendance d'après la seule hypothèse faite : toutes les distributions sont équiprobables.
(Entendons-nous bien, je sais que c'est vrai et je peux donner un argument, mais j'en attends un de toi).
92 messages
- Page 3 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
