Plus petit multiple de 2018
Olympiades mathématiques, énigmes et défis
-
alice02
- Membre Naturel
- Messages: 56
- Enregistré le: 28 Aoû 2017, 16:28
-
 par alice02 » 16 Déc 2017, 09:45
par alice02 » 16 Déc 2017, 09:45
Quel est le plus petit multiple de
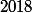
dont l’écriture décimale
commence par
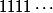
?
Répondez

si vous pensez qu’un tel multiple n’existe pas.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 16 Déc 2017, 10:35
par beagle » 16 Déc 2017, 10:35
0
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
alice02
- Membre Naturel
- Messages: 56
- Enregistré le: 28 Aoû 2017, 16:28
-
 par alice02 » 16 Déc 2017, 10:45
par alice02 » 16 Déc 2017, 10:45
Pourquoi?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2017, 11:16
par Ben314 » 16 Déc 2017, 11:16
Salut,
Je comprend pas ce que ça veut dire de "commencer par 1111....." avec des points de suspension.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 16 Déc 2017, 11:18
par beagle » 16 Déc 2017, 11:18
Ben314 a écrit:Salut,
Je comprend pas la question : est ce que le nombre cherché doit commencer par quatre "1" ou bien être entièrement composé de "1" ?
cela commence par 1111... mais les ... tu donnes ce que tu veux, c'est à ton bon cœur.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 16 Déc 2017, 11:20
par beagle » 16 Déc 2017, 11:20
alice02 a écrit:Pourquoi?
parce que je n'y arrive pas!
C'est pas valable comme réponse?
bon alors 2x5 = 10
et faut chopper une retenue pour faire le 11 de départ
oui mais 5x8= 40 donc je vais avoir 5+4 = 9 je n'arriverai pas à la fabriquer cette ptain de retenue.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2017, 11:24
par Ben314 » 16 Déc 2017, 11:24
Dans ce cas, c'est totalement couillon :
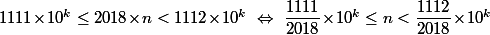
et il y a juste à calculer
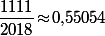
et
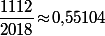
pour regarder quel est la première décimale qui diffère entre les deux.
Réponse : n=551 (et k=3) ;
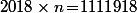
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 16 Déc 2017, 11:33
par beagle » 16 Déc 2017, 11:33
"c'est totalement couillon "
remarque cela en attrape quelques uns quand même!!!!
Bon pour ètre franc j'avais voulu effacer ma réponse 0.
Et je me suis gourré probablement dans la validation d'effacer ma réponse.
Après j'ai voulu justifié mon injustifiable!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2017, 11:37
par Ben314 » 16 Déc 2017, 11:37
Remarque qu'avec que des "1", c'est pas compliqué non plus vu que ça revient à chercher
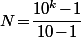
qui soit divisible par 2018, c'est à dire
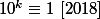
(vu que 9 est premier avec 2018).
Faut donc calculer l'ordre de 10 dans le groupe multiplicatif des éléments inversibles de Z/2018Z et c'est pas super long vu qu'on sait qu'il divise l'ordre du groupe, c'est à dire
)
(indicatrice d'Euler)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 16 Déc 2017, 11:51
par nodgim » 16 Déc 2017, 11:51
Sans le bagage du supérieur :
Il suffit de considérer le nombre 1111... 0000 (autant de 1 que l'on veut suivi de 4 zéros). Il y a forcément entre
1111...0000 et 1111....2018 un nombre divisible par 2018.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 16 Déc 2017, 11:59
par beagle » 16 Déc 2017, 11:59
nodgim a écrit:Sans le bagage du supérieur :
Il suffit de considérer le nombre 1111... 0000 (autant de 1 que l'on veut suivi de 4 zéros). Il y a forcément entre
1111...0000 et 1111....2018 un nombre divisible par 2018.
oui, nodgim
ceci devrait éviter de raconter n'importe quoi.
Encore un exo où j'ai manqué de retenue!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
alice02
- Membre Naturel
- Messages: 56
- Enregistré le: 28 Aoû 2017, 16:28
-
 par alice02 » 16 Déc 2017, 12:14
par alice02 » 16 Déc 2017, 12:14
Merci Ben314!

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités