Petit défi

[Darkwolftech]

Allez pour relancer la tradition (qui se perd un peu ...), un petit défi, que j'ai eu beaucoup de plaisir et qui m'a dégouté quand j'ai vu la simplicité de la solution :

On dit que deux nombres sont anagrammes l'un de l'autre lorsqu'on peut obtenir l'un à partir d'un permutation des chiffres de l'autre (exemple : 658 et 586). Attention, on ne compte pas les zéros "qui ne servent à rien" (exemple : 300 n'est pas l'anagramme de 003).

Deux puissances de 2 peuvent-elles anagrammes l'une de l'autre ?

Allez c'est pas compliqué pour vous .. :lol3:
Et surtout n'hésitez pas à proposer vos défis les plus intéressants, ça fait toujours plaisir !
Lucas

[nodjim]

Ce n'est pas possible, et ça se vérifie très facilement, rien qu'en observant le 1er et dernier chiffre.

[chan79]

salut
on peut montrer que deux puissances de 2 ne peuvent pas être égales modulo 9 si elles ont le même nombre de chiffres.

[Waax22951]

Bonjour,
J'y avais un peu réfléchis et j'étais aussi parti sur la somme des chiffres (apparemment certains m'ont devancé, mais ce n'est pas étonnant :ptdr: )

Un petit problème sur lequel j'étais jusqu'à ce soir:

Pour tout entier naturel non nul , il existe un unique réel positif 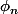qui vérifie:
[CENTER][/CENTER]
(Vous pouvez vous amuser à le montrer mais bon, c'est pas vraiment drôle à faire)

On définie ainsi la suite .

Montrer que:
[CENTER][/CENTER]

Bonne soirée ! :we:

[Robic]

L'hypothèse, je la lis ainsi : pour tout entier n>=1, il existe x unique solution positive de l'équation

Du coup pourquoi ne pas dire : pour tout entier n>=2, il existe x unique solution positive de l'équation ?

Cette existence semble facile à démontrer en étudiant la fonction , en notant que tandis que qui est strictement positif puisque n>=2. Par continuité et monotonie, f s'annule en un unique point (qui est >1 d'ailleurs).

Concernant l'étude de la limite, je me souviens avoir participé à une discussion où l'on s'intéressait à une suite de ce genre, peut-être celle-ci justement.

Ah, je l'ai retrouvée : http://www.maths-forum.com/showthread.php?t=153407&highlight=suite . Ce n'est pas tout à fait la même équation, mais je ne serais pas étonné si les mêmes méthodes s'appliquaient.

[DamX]

Hello,

ça m'a l'air plus simple que dans le fil que tu renvoies, en tout cas ça se fait facilement dans ce cas précis.

En effet considérer ta fonction f me semble plus qu'adapté.

Et tu remarques deux choses au sujet de f :
(tu l'as déja dit)

Et comme autre valeur intéressante tu peux prendre


Donc à partir d'un certain rang f(1+1/n)>0 et donc à partir de ce même rang la solution x_n est comprise entre 1 et 1+n (théorème valeurs intermédiaires).

Et donc x_n tend vers 1 (théorème des gendarmes).

Damien

[DamX]

Autre façon de faire sans même prendre une valeur particulière :

Soit x>1, on a

(avec f_n(x) = x^n-x-1)

et a fortiori :


ce qui donne une info sur la racine phi_n à partir de ce rang :

[Waax22951]

Je n'avais pas fait comme ça mais ça revient au même (en moins joli ^^)
D'ailleurs, DamX, j'aime beaucoup ta première méthode ! :lol3:

Sinon ma façon de faire était plus longue et moins belle:

(Je reprend la fonction )

On remarque que , puisque lorsque , on a:
, donc ne s'annule pas sur

Par ailleurs, on remarque que , qui est positive lorsque 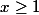, donc est croissante sur .

On a alors:
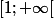, on a alors:


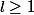D'où , ce qui est absurde. Donc . Or, puisqu'on a aussi , on peut affirmer que 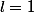, soit:

[CENTER][/CENTER]




Notons que ma façon de faire nécessite de montrer (en partie) l'unicité de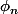 , ce qui n'est pas pratique du tout.. (C'est aussi un peu pour cela que je l'ai postée ^^)

Bonne après-midi !

[Waax22951]

L'hypothèse, je la lis ainsi : pour tout entier n>=1, il existe x unique solution positive de l'équation

Du coup pourquoi ne pas dire : pour tout entier n>=2, il existe x unique solution positive de l'équation

Si je ne l'ai pas écrit comme cela, c'est uniquement parce que je l'ai noté avec les "" sur mes brouillons: l'équation est évidente, mais le but de mon problème était de déterminer une famille de nombres qui vérifient une propriété similaire à . :lol3:

[Robic]

Ta démonstration est plus longue mais elle est intéressante aussi. En particulier j'aime bien ton idée de trouver l = 1 en commençant par exclure le cas l > 1.

[Fouzlui]

Merci d'arrêter de copier-coller cet exercice partout sur le forum et de consulter cette discussion afin de savoir comment poser ta question: http://www.maths-forum.com/poser-une-nouvelle-question-135053.php
Lostounet*