Loi de "l'étendu"
Olympiades mathématiques, énigmes et défis

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mar 2018, 14:26
par Ben314 » 12 Mar 2018, 14:26
Salut,
Comme y'a pas grand chose dans les énigmes/défi ces temps ci, j'en met une petite, moyennement dure et surtout moyennement drôle (c'est très "scolaire") :
Si
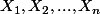
(
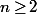
) sont des variables aléatoires indépendante de même loi uniforme sur [0,1], c'est quoi l'espérance de
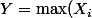-\min(X_i))
? sa variance ?
Modifié en dernier par
Ben314 le 12 Mar 2018, 16:10, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 12 Mar 2018, 15:02
par beagle » 12 Mar 2018, 15:02
je sais pas faire une soustraction, et alors?
Modifié en dernier par
beagle le 12 Mar 2018, 16:15, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Mar 2018, 15:42
par Lostounet » 12 Mar 2018, 15:42
Ben314 a écrit:Salut,
Comme y'a pas grand chose dans les énigmes/défi ces temps ci, j'en met une petite, moyennement dure et surtout moyennement drôle (c'est très "scolaire") :
Si
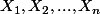
(
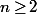
) sont des variables aléatoires indépendante de même loi uniforme sur [0,1], c'est quoi l'espérance
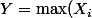-\min(X_i))
? sa variance ?
Salut,
Est-ce un truc comme:
 = n\int_0^1 {x^{n}dx} - n \int_0^1 {x(1-x)^{n-1}dx} = \frac{n}{n+1} - \frac{n}{n^2 + n})
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mar 2018, 16:07
par Ben314 » 12 Mar 2018, 16:07
Oui, pour l'espérance, c'est ça, modulo que tu t'es gouré dans la deuxième intégrale :
^{n-1}dx=\int_0^1(1-x)^{n-1}dx-\int_0^1(1-x)^{n}=\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{1}{n(n+1)})
et pas
(n+2)})
Donc
\!=\!\dfrac{n}{n+1}-\dfrac{1}{n+1}=\dfrac{n-1}{n+1})
(qui tend évidement vers 1)
Modifié en dernier par
Ben314 le 12 Mar 2018, 16:10, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Mar 2018, 16:08
par Lostounet » 12 Mar 2018, 16:08
Oui désolé, je rectifie !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Mar 2018, 16:29
par Lostounet » 12 Mar 2018, 16:29
Ben314 a écrit:Salut,
Comme y'a pas grand chose dans les énigmes/défi ces temps ci, j'en met une petite, moyennement dure et surtout moyennement drôle (c'est très "scolaire") :
Si
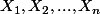
(
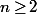
) sont des variables aléatoires indépendante de même loi uniforme sur [0,1], c'est quoi l'espérance de
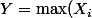-\min(X_i))
? sa variance ?
Pour la variance c'est un peu plus pénible avec la covariance du max et min. On pourrait regarder la loi conjointe... sauf s'il y a une "astuce".
Tu avais mis tout à l'heure je crois - une question sur "Xi qui suivent une loi normale".
Pour deux variables normales, il y avait un truc astucieux qui consistait à regarder E(U + V) (avec U le max et V le min) puis d'utiliser la loi demi-normale. Pour n variables je ne sais pas trop, à voir.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mar 2018, 16:37
par Ben314 » 12 Mar 2018, 16:37
Pour l'autre question (avec la loi normale), je l'ai enlevé vu que j'ai regardé dans le cas d'une loi quelconque ce qu'on pouvait écrire et que dans le cas de la loi normale (et n quelconque), j'ai pas l'impression qu'on ait une expression "simple" (i.e sans des tonnes d'intégrales non calculables de partout) de E(Y) et de V(Y).
Sinon, avec la loi uniforme, ben je connais pas d'astuce : perso j'ai calculé la loi conjointe du couple (Min,Max). (et c'est ce que j'avais dit : c'est très "scolaire"...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Mar 2018, 16:59
par Lostounet » 12 Mar 2018, 16:59
Ben314 a écrit:Pour l'autre question (avec la loi normale), je l'ai enlevé vu que j'ai regardé dans le cas d'une loi quelconque ce qu'on pouvait écrire et que dans le cas de la loi normale (et n quelconque), j'ai pas l'impression qu'on ait une expression "simple" (i.e sans des tonnes d'intégrales non calculables de partout) de E(Y) et de V(Y).
Sinon, avec la loi uniforme, ben je connais pas d'astuce : perso j'ai calculé la loi conjointe du couple (Min,Max). (et c'est ce que j'avais dit : c'est très "scolaire"...)
Petite révision (pour moi).. est-ce correct?
Si n = 2, pour le cas loi normale, si

et

suivent la loi N(0 ; 1), alors posons
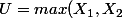)
et
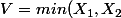)
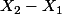
est combinaison linéaire de deux N(0 ; 1) indépendantes, on aurait donc que cette différence suit N(0 ; 2) et donc
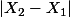
suit la loi demi-normale de variance

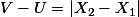
 = \frac{2}{\sqrt{\pi}})
?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
aviateur
 par aviateur » 12 Mar 2018, 23:49
par aviateur » 12 Mar 2018, 23:49
Bonsoir
j'ai calculé la densité de Y comme cela on a tout:
On a dc
=n(n-1)(1-x)x^{n-2})
On retrouve alors
=(n-1)/(n+1))
(qui tend vers 1 ...ok)
et
=\dfrac{2 (n-1)}{(1+n)^2 (2+n)})
(qui tend vers 0, interprétation???)
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 13 Mar 2018, 09:02
par beagle » 13 Mar 2018, 09:02
aviateur a écrit:Bonsoir
................et
=\dfrac{2 (n-1)}{(1+n)^2 (2+n)})
(qui tend vers 0, interprétation???)
ben plus on va vers les extrêmes, moins tu peux fluctuer, non
vers l'infini calé près de 0 et près de 1 pour les min et les max, ben ils sont à l'étroit pour bouger.
Par contre pourquoi 2 sur racine carrée de pi dépasse 1 pour le n=2 de gauss de Lostounet?
ah oui loi normale centrée reduite c'est ça?
du coup on ne peut pas comparer avec la loi uniforme sur [0,1]?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Mar 2018, 09:30
par Ben314 » 13 Mar 2018, 09:30
Je trouve la même chose (pour la densité, la moyenne et la variance).
Et a mon avis, l'interprétation, c'est celle que donne Beagle : si n est grand le Min est "quasi-sûrement" très proche de 0, et le Max de 1 donc une moyenne quasi égale à 1 et un écart type quasi égal 0.
Par contre, pourquoi l'écart type est en O(1/n), là, je sais pas trop...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 13 Mar 2018, 10:05
par beagle » 13 Mar 2018, 10:05
On peut pas avoir la loi normale sur [0,1] ?
Pour comparer
Lostounet on peut décentrer pour avoir n=2 sur [0,1]?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 13 Mar 2018, 10:57
par Lostounet » 13 Mar 2018, 10:57
beagle a écrit:On peut pas avoir la loi normale sur [0,1] ?
Pour comparer
Lostounet on peut décentrer pour avoir n=2 sur [0,1]?
La loi normale a pour support la droite réelle R par définition.
Alors que la loi uniforme a pour support le segment [0;1] ou [a;b]
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 13 Mar 2018, 11:18
par beagle » 13 Mar 2018, 11:18
Lostounet a écrit: beagle a écrit:On peut pas avoir la loi normale sur [0,1] ?
Pour comparer
Lostounet on peut décentrer pour avoir n=2 sur [0,1]?
La loi normale a pour support la droite réelle R par définition.
Alors que la loi uniforme a pour support le segment [0;1]
c'est sur que cela me faisait mal de l'écrire avec des [ ] bien fermés,
bon mais si par exemple on dit que la taille des hommes ou d'un type de poisson suit "pratiquement une courbe de Gauss, le poisson peut pas avoir une taille négative, ni faire 1 km de long.
Donc on peut pas tirer sur du [0,1] avec une distribution aléatoire gaussien? enfin s'approcher de...
Parce que après la bourde du jour d'hier, j'avais envie de tenter ma chance de nouveau aujourd'hui
sur la comparaison attendue des E et V selon loi uniforme ou loi normale.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 13 Mar 2018, 12:38
par beagle » 13 Mar 2018, 12:38
Bon alors voilà l'idée.
On prend une Gauss moyenne 0,5 entre 0 et 1
et on dit écart-type ben on peut prendre deux essais:
un avec 4 écarts-types de chaque coté donc 0,125
un avec 5 écart-types de chaque coté donc 0,1
et on fait idem loi uniforme.
avec l'idée, on attend à n égal une E plus faible et une V plus forte pour Gauss.
Vrai-faux , normal?
voire pour une E donné (donc des n différents), V reste plus élevée pour Gauss.
vrai -encore plus faux que l'autre , moins normal?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
aviateur
 par aviateur » 13 Mar 2018, 19:38
par aviateur » 13 Mar 2018, 19:38
Bonjour
J'ai regardé la même question avec la loi normale.
Avec la loi normale, il s'agit de comparer avec la loi uniforme si on a par exemple E(Y) tend vers + infini quand n tend vers l'infini.
Malheureusement si la démarche est la même pour le calcul de la densité de Y, je n'arrive pas à avoir d'expression simple pour cette densité..... pour moi c'est encore une énigme.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 13 Mar 2018, 19:52
par beagle » 13 Mar 2018, 19:52
Perso m'intéressait le retard de Gauss lié à sa concentration à la moyenne, et l'influence sur la variance.
mais aussi peut-ètre intéressant puisque Gauss va déborder le [0,1]
si gauss est en retard, à partir de quel n va-t-il dépasser le E= 1 max de l'uniforme sur [0,1], si on prend comme j'ai dit loi normale moyenne 0,5 et écart-type 0,1 ce qui fait du 5 écarts-type de chaque coté ppour prendre un exemple.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Mar 2018, 21:11
par Ben314 » 13 Mar 2018, 21:11
aviateur a écrit:Malheureusement si la démarche est la même pour le calcul de la densité de Y, je n'arrive pas à avoir d'expression simple pour cette densité..... pour moi c'est encore une énigme.
Perso, j'ai trouvé ça :
Si les

ont pour densité

(supposée "régulière" sur

) alors

:
- a pour fonction de répartition
\!=\!n\int_ {\mathbb R}f(x)\Big(\int_{x}^{x+y}\!\!f(t)\,dt\Big)^{n-1}\!\!\!dx)
- a pour densité
\!=\!n(n-1)\int_ {\mathbb R}f(x)f(x+y)\Big(\int_{x}^{x+y}\!\!f(t)\,dt\Big)^{n-2}\!\!\!dx)
.
Donc pour la gaussienne ET n=2, effectivement, c'est pas super archi méchant, mais pour
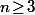
, là . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 14 Mar 2018, 15:11
par aviateur » 14 Mar 2018, 15:11
Oui j'ai donc la même remarque.
Néanmoins pour n fixé on peut calculer numériquement E(Y) et V(Y). Voir ci dessous
)
Pour n=2 on retrouve le résultat de @Lostounet car
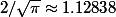

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mar 2018, 16:09
par Lostounet » 14 Mar 2018, 16:09
aviateur a écrit:Oui j'ai donc la même remarque.
Néanmoins pour n fixé on peut calculer numériquement E(Y) et V(Y). Voir ci dessous
)
Pour n=2 on retrouve le résultat de @Lostounet car
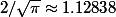
Sauf erreur de ma part, ma méthode semble aussi marcher pour n = 3 !
En utilisant des formules explicites fournissant le max(a;b;c) et min(a;b;c) pour trois réels a b et c, on a:
 - min(X_1,X_2,X_3) = \frac{|X_1 - X_2| + |X_2 - X_3| + |X_3 - X_1| }{2})
Par passage à l'espérance:
 = \frac{6}{2\sqrt{\pi}} = 1.6925687...)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
(
) sont des variables aléatoires indépendante de même loi uniforme sur [0,1], c'est quoi l'espérance
? sa variance ?
(
) sont des variables aléatoires indépendante de même loi uniforme sur [0,1], c'est quoi l'espérance de
? sa variance ?
(qui tend vers 0, interprétation???)