Loi de composition interne C1 sur R

[Ben314]

Salut,
Un petit défi pour ceux qui ne connaissent pas déjà :

Soit une loi de composition interne sur telle que soit un groupe et telle que soit de classe sur .
Montrer que est commutative.

[ffback]

Salut:
Par ici

[Ben314]

Salut:
Par ici

Effectivement (et la continuité suffit...)
Sinon, qu'est ce que tu fout, tu as pas retrouvé ton adresse mail et/ou et MdP pour te reconnecter sur le nouveau serveur ?

[ffback]

Il parait que les anciens Mdp sont irrécupérables, et l'email que j'ai utilisé á l'époque est lui aussi, irrécupérable...Pas grave, ça me fait une nouvelle jeunesse

Sinon, je suppose que le "vrai exo" caché de ton énoncé est "montrer que est -isomorphe á "
(á moins que tu aies une preuve directe de la commutativité?). Ainsi énoncé, ce n'est pas une conséquence claire de la version continue du lien

[Ben314]

Oui, la preuve que j'avais retrouvé sur un vieux truc, c'est effectivement de montrer que c'est isomorphe à (R,+) et d'en déduire la commutativité.
Je vais regarder si j'arrive à finir la preuve de l'autre post. concernant la continuité de x->x*x (aussi bien je l'avais déjà fait à l'époque : je sais plus...)

[ffback]

Je crois me souvenir que la continuité de x->x*x n'était pas trop dur á prouver, mais je te laisse vérifier ça

Sinon, autre question qui m'interesse: quid sur C au lieu de R? Est-ce que toutes les lois continues sur C (éventuellement avec de la régularité, eventuellement supposées commutatives) sont isomorphes á (C,+)?

[Ben314]

Effectivement, la continuité est assez évidente en utilisant la monotonie des "fonctions partielles" (c'est d'ailleurs ce que disait Doraki).
Sinon, sur C=R², vu que tu peut faire agir (R,+) sur le groupe des automorphismes de (R,+) via l'application x->(y->exp(x).y), tu peut construire un produit semi direct :
( x , y ) # ( x' , y' ) = ( x+exp(y).x' , y+y' )
qui est C^infini mais non commutatif donc (R²,#) n'est pas isomorphe à (R²,+).

Par contre, en supposant au départ que le groupe est commutatif (et de loi est "régulière"), ben... je sais pas...

[ffback]

Bien vu le contrexemple en non commutatif!
Il est possible qu'il n y ait pas beaucoup d'autres contrexemples que ça, mais restreignons nous donc au cas commutatif pour commencer.

Malheureusement, l'étude du probleme semble demander de s'y connaitre en topologie de R^n, ce qui n'est pas trop mon cas. Mais voilá quelques pistes:

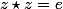
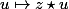
-L'équation (e=le neutre) n'a pas de solutions autre que z=e: en effet, cette équation signifie que l'aplication est une involution de C, et un résultat de topo (que je sais pas montrer...) dit qu'une involution continue du plan a nécessairement un point fixe, ce qui n est pas le cas si z est différent de e.

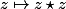
-Comme on est dans le cas commutatif, ça implique que est injective.

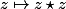
-Un autre résultat de topo que je sais pas démontrer dit que le fait que est injective et continue implique que cette application est ouverte. Si on montre de plus par exemple que l'application est propre, ce qui ne semble pas déraisonnable, ça implique que l'application est aussi fermée, donc surjective et ce serait donc un homeo. On aurait donc une "racine carrée" á notre disposition.

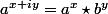
-On pourrait alors ensuite alors définir comme en dimension 1 les puissances dyadiques pour , puis étendre aux puissances réelles si tout se passe bien, puis peut être même des puissances complexes en posant pour b bien choisi.

PS:beaucoup de changements sur le forums, mais toujours pas de mode mathématique s'activant avec $...$

[ffback]

Autre idée, pour le cas régulier: construire des fonctions "puissance t", ça revient á fabriquer des fonctions t->z(t) vérifiant z(t+t')=z(t)*z(t'). Y'a peut être moyen de faire ça avec une équa diff

[Ben314]

Je suis tout a fait convaincu par le premier post. et ça me semble un bon départ.
Par contre, avec des équa. diff., soit on veut dériver directement par rapport à t (complexe) et il faut supposer que la loi est holomorphe (en une variable au minimum) ce qui est sacrément restrictif, soit on regarde ça comme une fonction de deux variables réelles et on va tomber sur une équation différentielle avec une fonction de deux variables ce qui risque de pas être super facile à manipuler (à voir...)

[ffback]

J'ai pas été assez précis dans mon dernier post: je propose de définir les fonctions z(t) pour t réel seulement. (donc équa diff standard), cad un morphisme de (R,+) dans (C,*). Aprés on étendrais aux complexes comme expliqué dans le premier post. On prend 2 fonctions construites ainsi z(t) et z1(t) "bien choisies", puis on pose:
,
et on espére que ça donne un isomorphisme.

[ffback]

J'ai réussi le cas le C2+commutatif, qui s'est avéré conceptuellement plus court que je ne le pensais. Ainsi:

Soit une loi sur telle que soit un groupe commutatif et telle que est de classe sur . Alors est isomorphe á .

Pour qui ça intéresse de chercher, voici les grandes étapes:

1)Pour tout de , il existe une unique fonction de classe telle que:

(Indication: dériver la relation désirée en s=0 pour former une équation différentielle)

2)Pour tous a,b dans ,

3)La fonction est un ismorphisme de sur .

[ffback]

Cas C^2 non commutatif sur R^2: je pense avoir obtenu que la loi donné par Ben est á isomorphisme prés la seule loi C^2 non commutative:
( x , y ) # ( x' , y' ) = ( x+exp(y).x' , y+y' )
Ainsi, il y a exactement deux classes d'isomorphismes pour les lois C^2 du plan, la classe des lois commutatives et celle des lois non commutatives.

(Mais á mon avis, je suis en train de réinventer la roue, et pour quelqu'un qui contrairement á moi s'y connait un petit peu en groupe de Lie tout ça doit être bien facile. Par ex, il me semble que le morphisme Phi que j'ai défini au post précédent et me suis fatigué á construire n'est autre que la fonction exponentielle du groupe de Lie ...)