Limite simple continue

[quinto]

Salut,
soit f la fonction caractéristique de Q dans R.
Existe il une suite de fonctions continues (f_n) convergeant vers f dans R?
Si oui en exhiber une, sinon pourquoi?

a+

[buzard]

Je pense que c'est faisable, je crois que cette suite fonctionne :

Je me limite à trouver des fonctions sur [0,1], puis il suffit de compléter par périodicité,



où est un triangle qui pointe à 1 en x=a et qui vaut 0 quand on s'éloigne de plus de h. On prend epsilon suffisement petit pour que les triangles ne se chevauche pas


Je note ^ et v respectivement le pgcd et le ppcm

Bon je crois que ca devrais marcher, à moins que je dise n'importe quoi ...

bon pour x rationnel ca marche, on a bien que f_n(x) = 1 à partir de n=denominateur.

pour x irrationnel . hmmm ...

[buzard]

zut je crois que ca va pas marcher. en faite le probleme, c'est que les meilleurs approximation rationnel sont à écarts majorés mais pas minoré.

Il y a surement des irrationnels qui sont tellement proche d'une de leur approximation qu'il deviens impossible de choisir un epsilon qui permette de le sortir de tous les triangles à partir d'un certain rang.

pour les nombres algébriques il n'y a pas de probleme, en gros vue qu'il possède de mauvaise approximation, il n'y aura qu'un nombre fini de rationnel assez pres :
|x-p/q|<1/q^(m+e) (m degree du polynome minimale de x)
ne possède qu'un nombre finis de solution donc en choisissant epsilon < 1/n^(n+1) on arrive à les sortirs des triangles à partir d'un certain rang.

Le vrai probleme ce sont les nombres transcendants, ils sont tellement bien approximable par des rationnel que les sortirs des triangles doit à mon avis etre impossible
|x-p/q|<1/q^m possède pour tout m une infinité de solution, ce qui veut dire qu'on ne pourras pas le séparer avec aucun epsilon de la forme 1/n^f(n)

so much ado about nothing,

ca veut pas dire que la suite cherchée n'existe pas, c'est tous simplement que ce n'est pas celle-là.

[quinto]

Salut,
effectivement, je pense que ca ne marchera pas. :)

[El_Gato]

Supposons qu'il existe une suite de fonctions continues qui converge simplement sur vers .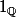

Plaçons nous sur un intervalle compact [a,b]. Pour chaque x de [a,b], il existe un voisinage ouvert tel que, , alors sur . Par compacité, il existe un recouvrement fini de [a,b] par ces ouverts. Alors, si pour tout x dans [a,b]. Donc on peut supposer que la suite est positive à partir d'un certain rang sur le compact [a,b].

Soit maintenant la suite de fonctions définie par:
sur [a,b]. La suite est croissante et positive à partir d'un certain rang sur [a,b]. De plus, chaque continue. Cette suite converge vers 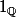puisque n'est autre que la limite inf des .

Alors, par le théorème de Fatou
. Les étant positives et continues, cela impliquerait sur [a,b]. Impossible.

[El_Gato]

Supposons qu'il existe une suite de fonctions continues qui converge simplement sur vers .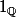

Plaçons nous sur un intervalle compact [a,b]. Pour chaque x rationnel de [a,b], il existe un voisinage ouvert tel que, , alors sur . Par compacité, il existe un recouvrement fini de [a,b] par ces ouverts. Alors, si pour tout x dans [a,b]. Donc on peut supposer que la suite est positive à partir d'un certain rang sur le compact [a,b].

Soit maintenant la suite de fonctions définie par:
sur [a,b]. La suite est croissante et positive à partir d'un certain rang sur [a,b]. De plus, chaque continue. Cette suite converge vers 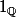puisque n'est autre que la limite inf des .

Alors, par le théorème de Fatou:
, et c'est une convergence croissante. Les étant positives et continues, cela impliquerait sur [a,b] à partir d'un certain rang.

Impossible.

Conclusion: il n'existe pas de suite de fonctions continues qui converge simplement sur la droite vers la fonction caractéristique des rationnels.

[El_Gato]

Aie ! Je viens de me rendre compte d'une erreur dans mon raisonnement précédent: on ne peut pas imposer à tous les , pour , d'être positives sur le même .

Du coup je ne sais plus. Je vais voir si la preuve précédente peut être rectifiée.

[El_Gato]

Je crois avoir trouvé. Ma dernière solution était incomplète.
Solution complète.

Supposons qu'il existe une une suite de fonctions continues qui converge simplement vers la fonction caractéristique des rationnels .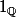

On se place sur un compact [a,b]. Soit un réel assez petit. Soit x un rationnel de [a,b].

Il existe tel que implique . Donc si , est un ouvert non vide autour de x. Ces ouverts forment un recouvrement de [a,b].

Puisque [a,b] est compact, il existe un sous recouvrement fini . Alors, si , est dans pour tout x, c'est à dire positif.


Autrement dit, toutes les sont positives à partir d'un certain rang sur le compact [a,b].

On peut alors conclure comme dans ma première démonstration ci-dessus: on considère la suite de fonctions . C'est une suite croissante de fonctions continues, positives à partir d'un certain rang, qui converge simplement vers .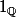

Par le théorème de Fatou, on conclut alors que , en croissant, donc que 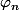devrait être nulle à partir d'un certain rang, puisque que chaque 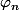est positive (pour n assez grand) et continue.

C'est impossible, donc il n'existe pas de suite de fonctions continues qui converge simplement vers la fonction caractéristique des rationnels.