telles que, pour tous réels
Fonction du produit et somme
5 messages
- Page 1 sur 1
fonction du produit et somme
Soit  l'ensemble des nombres réels. Déterminer toutes les fonctions
l'ensemble des nombres réels. Déterminer toutes les fonctions 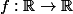
telles que, pour tous réels et
et  :
:
f(y)) + f(x + y) = f(xy).)
telles que, pour tous réels
Re: fonction du produit et somme
Salut,
Je pense qu'il n'y a que 3 solutions : f(x)=0 ; f(x)=x-1 et f(x)=1-x.
Je n'ai pas la preuve complète, mais un "bon début" pourrait être ça :
Cas 1 : S'il existe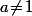 tel que
tel que \!=\!0) alors
alors 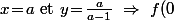\!+\!f(\frac{a^2}{a-1})\!=\!f(\frac{a^2}{a-1})\ \Rightarrow\ f(0)\!=\!0)
Puis,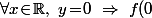\!+\!f(x)\!=\!f(0)\ \Rightarrow\ f(x)\!=\!0) .
.
Cas 2 : Si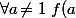\!\not=\!0) alors
alors 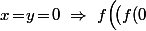)^2\!\Big)\!+\!f(0)\!=\!f(0)\ \Rightarrow\ f(0)\!=\!\varepsilon\!=\!\pm1\text{ et }f(1)\!=\!0)
Puis,\!+\!f(x\!+\!1)\!=\!f(x)\ \Rightarrow\ \forall n\!\in\!{\mathbb Z},\ f(x\!+\!n)\!=\!f(x)\!-\!n\varepsilon\ (\text{ donc }f(n)\!=\!(1\!-\!n)\varepsilon\ )) .
.
Je pense qu'il n'y a que 3 solutions : f(x)=0 ; f(x)=x-1 et f(x)=1-x.
Je n'ai pas la preuve complète, mais un "bon début" pourrait être ça :
Cas 1 : S'il existe
Puis,
Cas 2 : Si
Puis,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: fonction du produit et somme
Déjà, bonjour/bonsoir... On remercie Ben314 d'avoir donné une piste de réflexion et on essaie de chercher un peu de son côté, non ? Enfin, pourquoi parler en anglais ? Je te rappelle que tu es sur un site francophone. Si tu ne parles pas le français pourquoi faire des exos en français ? Et pourquoi ne pas aller sur un site où tu pourras mieux comprendre et éventuellement te faire comprendre ? La prochaine fois, ne poste pas en section "Défis et énigmes" si ton but est de nous faire faire tes devoirs à ta place...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: fonction du produit et somme
Dommage effectivement qu'alice02 se contente de mettre des énoncés.
Pour le cas où certains auraient continué à s'intéresser à ce sujet, on peut montrer rapidement que si une fonction f vérifie l'égalité donnée et l'égalité f(0)=1 et si elle est surjective, c'est nécessairement la fonction de dans
dans  : x --> 1-x
: x --> 1-x
Pour le cas où certains auraient continué à s'intéresser à ce sujet, on peut montrer rapidement que si une fonction f vérifie l'égalité donnée et l'égalité f(0)=1 et si elle est surjective, c'est nécessairement la fonction de
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
