Fonction zeta, somme et limites.
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 21:43
par Nightmare » 20 Déc 2010, 21:43
Hello,
un mélange de calcul de sommes et de limites :
On note pour x > 1
=\Bigsum_{k=1}^{\infty} \frac{1}{k^{x}})
(pour ceux pour qui ce n'est pas clair, on pourra d'abord montrer que
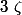
est bien définie)
Calculer :
1)
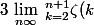 - n\))
2)
}{k}-ln(n)\))
Aucune connaissance sur la fonction zeta autre que sa définition, donnée dans l'énoncé, n'est requise.
:happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 21 Déc 2010, 00:05
par girdav » 21 Déc 2010, 00:05
Bonsoir,
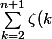 -n= \sum_{k=2}^{n+1}\sum_{j=2}^{+\infty}\fr 1{j^k}<br />= \sum_{j=2}^{+\infty}\sum_{k=2}^{n+1}\fr 1{j^k})
.
}\\<br />&= \fr 1{j(j-1)}-\fr 1{j^{n+1}(j-1)}.<br />\end{align})
On a que
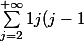} = 1)
et
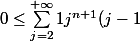}\leq \sum_{j=2}^{+\infty}\fr 1{j^n})
et cette dernière quantité tend vers

quand

tend vers l'infini. On en conclut que
-n =1})
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Déc 2010, 00:24
par Nightmare » 21 Déc 2010, 00:24
Ca me va :happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Déc 2010, 17:17
par benekire2 » 21 Déc 2010, 17:17
Salut nigtmare et girdav,
Bon, je vais voir ce que ça donne pour la question 2 qui m'a l'air plus dur que la première du fait que l'on peu pas passer le ln(n) dans la somme très facilement.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Déc 2010, 17:30
par Nightmare » 21 Déc 2010, 17:30
Oublie pas ce que tout le monde appelle le "télescopage" !
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Déc 2010, 17:56
par benekire2 » 21 Déc 2010, 17:56
Nightmare a écrit:Oublie pas ce que tout le monde appelle le "télescopage" !
Ok ,
on pourrais essayer de faire apparaître la première question dedans ?
-
ppcrepin
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Juil 2010, 19:11
-
 par ppcrepin » 31 Déc 2010, 18:55
par ppcrepin » 31 Déc 2010, 18:55
il faut sans doute utiliser que la somme des 1/k pour k allant de 1 à n est équivalente à ln(n) quand n tend vers + infini
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
(pour ceux pour qui ce n'est pas clair, on pourra d'abord montrer que
est bien définie)
