Un produit en somme
Olympiades mathématiques, énigmes et défis
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 28 Déc 2008, 17:53
par Imod » 28 Déc 2008, 17:53
Bonjour :we:
Encore une énigme ouverte à tous :zen:
Pour tout entier

supérieur à 0 on note

. Comment choisir

pour que l'on puisse partitionner

en deux sous-ensembles

et

tels que la somme des éléments de

soit égale au produit des éléments de

?
Par exemple
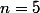
convient en effet :

et

. En effet

,

et

.
Bon courage !
Imod
-
Kah
- Membre Rationnel
- Messages: 540
- Enregistré le: 15 Sep 2008, 19:51
-
 par Kah » 28 Déc 2008, 17:59
par Kah » 28 Déc 2008, 17:59
Il faut le cas general?
Si oui, trop ardu pour moi :we:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 28 Déc 2008, 18:16
par Imod » 28 Déc 2008, 18:16
Kah a écrit:Il faut le cas general?
Oui mais rien n'empêche de commencer tranquillement par les premières valeurs de

:zen:
Imod
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 29 Déc 2008, 09:14
par nodgim » 29 Déc 2008, 09:14
Factorisation gràce à l'as! :++:
-
jeancam
- Membre Relatif
- Messages: 171
- Enregistré le: 07 Nov 2008, 21:54
-
 par jeancam » 29 Déc 2008, 12:29
par jeancam » 29 Déc 2008, 12:29
on peut avoir P formé de l as ;-),p et q
on ecrit n(n+1)/2-p-q-1=pq
et on factorise
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Déc 2008, 12:38
par lapras » 29 Déc 2008, 12:38
Salut,
On remarque que pour les 1eres valeurs de n, le produit est composé de 3 éléments : 1, a , b.
On cherche donc n tel que :
(1+...+n)-(1+a+b)=a*b*1=ab
ce qui équivaut à
n(n+1)=2(a+1)(b+1)
si n impair, il suffit de prendre
a=n
b=(n-1)/2
si n pair, il suffit de prendre b=(n-2)/2 et a=n.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Déc 2008, 12:43
par lapras » 29 Déc 2008, 12:43
Grillé :we:
-
jeancam
- Membre Relatif
- Messages: 171
- Enregistré le: 07 Nov 2008, 21:54
-
 par jeancam » 29 Déc 2008, 12:45
par jeancam » 29 Déc 2008, 12:45
quels sont les valeurs de n pour lesquels il y a d autre partitions ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Déc 2008, 12:53
par lapras » 29 Déc 2008, 12:53
Quel est le nombre f(n) de partitions ?
-
jeancam
- Membre Relatif
- Messages: 171
- Enregistré le: 07 Nov 2008, 21:54
-
 par jeancam » 29 Déc 2008, 13:07
par jeancam » 29 Déc 2008, 13:07
lapras a écrit:Quel est le nombre f(n) de partitions ?
par convention f(1)=1 ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Déc 2008, 13:19
par lapras » 29 Déc 2008, 13:19
Disons n
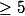
J'ai ma petite idée je met ca au clair pour ce soir...
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 29 Déc 2008, 16:35
par Imod » 29 Déc 2008, 16:35
lapras a écrit:si n impair, il suffit de prendre
a=n-1 et b=(n-1)/2
si n pair, il suffit de prendre b=(n-2)/2 et a=n.
Attention quand même , quand n=1;2 ou 3 il n'est pas possible que P ait 3 éléments et pour n=4 ,

impossible . En fait il n'y a pas de solution pour n=1;2;4 et pour n=3 :

et

.
Pour l'unicité je ne me suis pas posé la question :we:
Imod
-
jeancam
- Membre Relatif
- Messages: 171
- Enregistré le: 07 Nov 2008, 21:54
-
 par jeancam » 29 Déc 2008, 19:00
par jeancam » 29 Déc 2008, 19:00
Imod a écrit:. En fait il n'y a pas de solution pour n=1;2;4 :we:
Imod
si tu considere que le produit de zero nombre est 1 il y a une solution pour n=1
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Déc 2008, 19:07
par lapras » 29 Déc 2008, 19:07
Oui enfin on va pas chipoter ;)
-
jeancam
- Membre Relatif
- Messages: 171
- Enregistré le: 07 Nov 2008, 21:54
-
 par jeancam » 29 Déc 2008, 19:21
par jeancam » 29 Déc 2008, 19:21
lapras a écrit:Oui enfin on va pas chipoter

tu m ote les mots de la bbouches;-))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités