Etudier la continuïté d"une fonction.
Olympiades mathématiques, énigmes et défis
-
aviateur
 par aviateur » 30 Sep 2017, 16:00
par aviateur » 30 Sep 2017, 16:00
Bonjour
Soit f définie sur

par
=1)
si

=0)
si

=1/q)
si
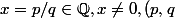=1.)
Déterminer le domaine de continuité de f.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Sep 2017, 16:08
par Ben314 » 30 Sep 2017, 16:08
Salut,
Elle est clairement discontinue en tout point x rationnel vu que f(x) est non nul et qu'il existe des irrationnels y aussi proche qu'on veut de x qui vérifient f(y)=0.
C'est un peu moins clair, mais en fait elle est continue en tout x irrationnel car si on fixe un epsilon>0, il ne va clairement y avoir qu'un nombre fini de fraction p/q dans ]x-1,x+1[ telles que q<=1/epsilon donc on peut trouver un intervalle ouvert centré en x qui n'en contient aucune ce qui signifie que pour tout y de cet intervalle (rationnel ou pas), on aura f(y)<epsilon (si y=p/q est rationnel, on aura q>1/epsilon vu que par construction aucun p/q tel que q<1/epsilon n'est dans l'intervalle et on en déduit que f(y)=1/q<epsilon)
Question : existe-t-il réciproquement une fonction f:R->R qui soit continue en tout x rationnel et discontinue en tout x irrationnel ? (c'est à dire dont le "domaine de continuité" soit exactement Q si tu préfère)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 30 Sep 2017, 16:30
par Lostounet » 30 Sep 2017, 16:30
Ben314 a écrit:)
Question : existe-t-il réciproquement une fonction f:R->R qui soit continue en tout x rationnel et discontinue en tout x irrationnel ? (c'est à dire dont le "domaine de continuité" soit exactement Q si tu préfère)
De mémoire, en appliquant le théorème de Baire.. on peut montrer par l'absurde que si le domaine de continuité Q (si f est supposée existante) s'écrivait comme intersection dénombrable d'ouverts, alors en prenant leur complémentaire on vérifie qu'ils sont d'intérieurs vides (comme les irrationnels)
[...]
Puis en écrivant R=(irrationnels)U(rationnels) on aboutit au fait que R est réunion dénombrable de fermés d'intérieurs vides. Quelques chose comme ça..ou pas du tout? J'ai un doute sur les [...]
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Sep 2017, 17:32
par Ben314 » 30 Sep 2017, 17:32
C'est bien ça :
On montre facilement que l'ensemble de continuité C d'une fonction de R->R, c'est forcément une intersection d'ouverts de R (il suffit de bien regarder la définition de "être continue en xo")
Et si on avait C=Q donc Q=intersection dénombrable d'ouverts, ben déjà, ça prouverais que tout les ouverts en question sont dense (vu qu'il contiennent Q) et ensuite en faisant l'intersection de ces ouverts là avec les R\{x_o} [xo dans Q], ben ça nous ferait au total une intersection dénombrable [dénombrable + dénombrable = dénombrable] d'ouverts denses de R qui serait vide et ça, même si on ne connait pas la théorie de Baire, c'est facile de montrer que c'est pas possible.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 30 Sep 2017, 17:58
par aviateur » 30 Sep 2017, 17:58
Ok c'est bien.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités