Equation diophantienne
Olympiades mathématiques, énigmes et défis
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 22 Aoû 2008, 12:42
par acoustica » 22 Aoû 2008, 12:42
Bonjour à tous, voici un nouveau problème:
Résoudre l'équation diophantienne suivante dans N:

voilavoila, enjoy yourself! :happy2:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Aoû 2008, 14:30
par Zweig » 22 Aoû 2008, 14:30
Salut,
Les grandes lignes (sauf erreurs) :
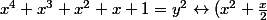^2 + \frac{3x^2}{4} + x + 1 = y^2)
Or,
^2 < x^4 + x^3 + x^2 + x + 1 < (x^2 + \frac{x}{2}+2)^2)
. On en déduit alors
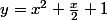
. On subtitue ça dans l'équation initial et on trouve quelques solutions.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 22 Aoû 2008, 14:34
par acoustica » 22 Aoû 2008, 14:34
Zweig a écrit:Salut,
Les grandes lignes (sauf erreurs) :
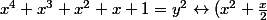^2 + 3x^2 + x + 1 = y^2)
Or,
^2 < x^4 + x^3 + x^2 + x + 1 < (x^2 + \frac{x}{2}+2)^2)
. On en déduit alors
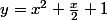
. On subtitue ça dans l'équation initial et on trouve quelques solutions.
Zweig, on peut compter sur toi! :jap:
Tu propose un autre problème? :+++:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 22 Aoû 2008, 14:51
par Doraki » 22 Aoû 2008, 14:51
Zweig,
(x²+x/2+1)² est plus grand que 1+x+x²+x³+x^4 à partir de x>0, donc ça permettrait de dire qu'il n'y a pas d'autre solution avec ton argument ?
Ton post dit un truc marrant quand on prend x impair.
Par contre, (x²+(x+1)/2)² est plus grand que 1+x+x²+x³+x^4 à partir de x>3 ça permet de dire qu'il n'y a que 2 solutions (x=0 et x=3)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 22 Aoû 2008, 15:19
par acoustica » 22 Aoû 2008, 15:19
Doraki a écrit:Zweig,
(x²+x/2+1)² est plus grand que 1+x+x²+x³+x^4 à partir de x>0, donc ça permettrait de dire qu'il n'y a pas d'autre solution avec ton argument ?
Ton post dit un truc marrant quand on prend x impair.
Par contre, (x²+(x+1)/2)² est plus grand que 1+x+x²+x³+x^4 à partir de x>3 ça permet de dire qu'il n'y a que 2 solutions (x=0 et x=3)
On a [TEX] (x^2+\frac{x}{2})3, donc pas de solutions.
Pour x=0, 1 ou 2 ou 3, c'est du cas par cas.
Cela répond-il à ta question? :happy2:
Edit: oups c'est exactement ce que tu viens d'écrire, dsl
Bon, bah...il aura pas duré longtemps celui-là
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 22 Aoû 2008, 19:13
par acoustica » 22 Aoû 2008, 19:13
Bon, tant pis je propose un petit truc pas sorcier:
Résoudre l'équation diophantienne dans Z:
^4=c^2)
voilavoila :we:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Aoû 2008, 20:07
par Zweig » 22 Aoû 2008, 20:07
Sauf erreurs :
^4 < a^4 + b^4 + (a + b)^4 < (a + b + 1)^4)
L'équation n'admet donc aucune solution.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Aoû 2008, 20:18
par leon1789 » 22 Aoû 2008, 20:18
acoustica a écrit:Bon, tant pis je propose un petit truc pas sorcier:
Résoudre l'équation diophantienne dans Z:
^4=c^2)
voilavoila :we:
Solution 100% algébrique :
Soit a,b,c un triplet solution dans Z^3.
L'égalité
^4=c^2)
force
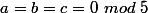
Alors, en divisant par 5^4, il vient
^4+(b/5)^4+((a+b)/5)^4=(c/25)^2)
donc a/5,b/5,c/25 est aussi solution dans Z^3.
Quels sont les entiers divisibles infiniment par 5 et/ou 25 ? il n'y a que 0.
D'où l'unique solution a=b=c=0

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Aoû 2008, 20:23
par leon1789 » 22 Aoû 2008, 20:23
PS : le même principe fonctionne aussi avec une réduction modulo 11 ! :id:
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 22 Aoû 2008, 21:27
par acoustica » 22 Aoû 2008, 21:27
leon1789 a écrit:L'égalité
^4=c^2)
force
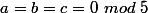
Tu peut détailler ce passage s'il te plait? Je ne comprend pas. Sinon, bonne idée la descente infinie. :id:
Sinon, ce n'est pas le plus efficace, avec une factorisation du type
^4=2*X^2)
, c'est fini :++: . (mais le coup des modulos, je suis quand même curieux, ça peut être une bonne méthode à retenir)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Aoû 2008, 21:34
par leon1789 » 22 Aoû 2008, 21:34
acoustica a écrit:Tu peut détailler ce passage s'il te plait?
pour tout premier

, on a
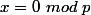
ou bien
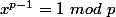
. Ici, on prend p=5, si bien que les puissances 4-ièmes disparaissent littéralement, se transformant en 0 ou 1 !
Ensuite, modulo 5,

.
acoustica a écrit:Sinon, ce n'est pas le plus efficace, avec une factorisation du type
^4=2*X^2)
, c'est fini.
Si, c'est mieux, mais il fallait le voir :zen:
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 22 Aoû 2008, 21:36
par acoustica » 22 Aoû 2008, 21:36
leon1789 a écrit:Si, c'est mieux, mais il fallait le voir :zen:
Après coup, oui c'est vrai c'est mieux
Merci pour le détail :happy2:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Aoû 2008, 21:48
par leon1789 » 22 Aoû 2008, 21:48
Je propose une autre équation à résoudre sur Z :
^2 = a^2(4b-a^2))
Je la donne comme ça (je connais quand même le résultat), mais je ne sais pas ce qu'elle vaut niveau difficulté.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 23 Aoû 2008, 08:42
par acoustica » 23 Aoû 2008, 08:42
^2+(a^2)^2=4ba^2)
d'où
^2=2a^2(2b+1+b^2)=2(a(1+b))^2)
donc pas de solution, sauf erreur de calcul.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 23 Aoû 2008, 09:08
par Doraki » 23 Aoû 2008, 09:08
(1-b²)² = (1+b²)²-4b² = -a^4 +4a²b -4b² = -(a²-2b)²
Donc il faut 1-b² = a-2b = 0, donc b²=1 et a²=2b, et de là on voit qu'il n'y a pas de solution dans Z.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Aoû 2008, 11:42
par leon1789 » 23 Aoû 2008, 11:42
oki :++: pas mieux de mon coté
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 23 Aoû 2008, 12:57
par acoustica » 23 Aoû 2008, 12:57
Allez, je poste mon dernier problème.
Trouver tous les nombres entiers positifs x et y de telle sorte que
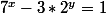
:we:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 23 Aoû 2008, 14:05
par Zweig » 23 Aoû 2008, 14:05
Les seuls couples solution sont (1,1) et (2,4). Je posterais ma solution plus tard.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 23 Aoû 2008, 14:50
par acoustica » 23 Aoû 2008, 14:50
Zweig a écrit:Les seuls couples solution sont (1,1) et (2,4). Je posterais ma solution plus tard.
C'est exact.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 23 Aoû 2008, 20:16
par acoustica » 23 Aoû 2008, 20:16
Zweig a écrit:Les seuls couples solution sont (1,1) et (2,4). Je posterais ma solution plus tard.
En attendant ta solution, c'est exact! :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
force
, c'est fini.