Enigme bien corsée!
Olympiades mathématiques, énigmes et défis
-
charlattend
- Messages: 3
- Enregistré le: 04 Juin 2007, 15:36
-
 par charlattend » 04 Juin 2007, 15:45
par charlattend » 04 Juin 2007, 15:45
J'ai une énigme bien corsée sur laquelle je bloque depuis plusieurs jours:
Trouver le nombre manquant de cette suite logique :
10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18 - 21 - 23 - 25 - X - 101 - 122 - 10001
J'ai pensé aux systèmes de changements de bases, mais même avec ca je trouve pas, des idées?
Pour ceux qui sont interessés, j'ai tiré cette énigme d'un site qui en propose une ENORME base de donnée, la plupart étant très mathématiques, si ca vous interesse c'est sur:

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 16:02
par aviateurpilot » 04 Juin 2007, 16:02
10, 11, 12, 13, 14, 15, 16, 17, 18, 21, 23, 25, 32, 101, 122, 10001,
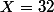
)+\bigsum_{i=0}^{+\infty}10^{i+1}E\(\frac{17}{(18-n)^i}\)})
-
charlattend
- Messages: 3
- Enregistré le: 04 Juin 2007, 15:36
-
 par charlattend » 04 Juin 2007, 16:14
par charlattend » 04 Juin 2007, 16:14
Ok merci pour la réponse, mais pourquoi 32?
Tu es en mathsup toi aussi ;)?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 16:19
par aviateurpilot » 04 Juin 2007, 16:19
charlattend a écrit:Ok merci pour la réponse, mais pourquoi 32?
Tu es en mathsup toi aussi

?
oui ,je suis en mathsup

dans la formule que je t'ai donné
-
charlattend
- Messages: 3
- Enregistré le: 04 Juin 2007, 15:36
-
 par charlattend » 04 Juin 2007, 16:23
par charlattend » 04 Juin 2007, 16:23
Merci bcp, mais par contre euh tu la sors d'ou cette formule? Car elle me semble pas évidente au premier coup d'oeil comme ca, tu l'avais deja faite cette énigme ou tu as trouvé ca comme ca^^?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 16:34
par aviateurpilot » 04 Juin 2007, 16:34
charlattend a écrit:Merci bcp, mais par contre euh tu la sors d'ou cette formule? Car elle me semble pas évidente au premier coup d'oeil comme ca, tu l'avais deja faite cette énigme ou tu as trouvé ca comme ca^^?
meme si la relation n'est pas evident,
mais la facon avec la quel j'ai trouvé cette formule n'est pas aussi difficile
17 dans la base 17=10
17 dans la base 16=11
17 dans la base 15=12
...
...
17 dans la base 9=18
17 dans la base 8=21
17 dans la base 7=23
17 dans la base 6=25
17 dans la base 5=32
17 dans la base 4=101
17 dans la base 3=122
17 dans la base 2=1001
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Juin 2007, 18:20
par fahr451 » 05 Juin 2007, 18:20
bestial aviateur pilote
j'avoue que je n'ai absolument pas l'esprit entrainé pour ce genre de suites logiques je pense cependant qu'en "pratique" il y a un nombre fini de situations classiques et qu'il suffit de les avoir vues toutes enfin j'espère
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 05 Juin 2007, 19:24
par aviateurpilot » 05 Juin 2007, 19:24
fahr451 a écrit:bestial aviateur pilote
j'avoue que je n'ai absolument pas l'esprit entrainé pour ce genre de suites logiques je pense cependant qu'en "pratique" il y a un nombre fini de situations classiques et qu'il suffit de les avoir vues toutes enfin j'espère
j'aime pas travailler les livres d'exos pour voir le maximum de situations,
c'est quoi "bestial" lol, et dsl si je questionne bcp sur la langue.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités

