Salut,
Montrer que tout rationnel peut s'écrire comme la somme de 3 cubes de rationnels.
Ecriture d'un rationnel
10 messages
- Page 1 sur 1
par acoustica » 01 Jan 2009, 21:56
Zweig a écrit:Salut,
Montrer que tout rationnel peut s'écrire comme la somme de 3 cubes de rationnels, distincts et non nuls.
http://www.animath.fr/IMG/pdf/cours-base2.pdf
en bas de la page 15 :we:
euh... franchement, comment peut-on le trouver? A moins qu'il y ait une autre solution?
par Zweig » 01 Jan 2009, 22:05
Ah, tiens je ne le connaissais pas ce poly ! Tu l'as trouvé comment ? Car le seul poly que j'ai sur les stratégies de base c'est un truc tout simple, celui-là est vachement développé !
par lapras » 02 Jan 2009, 13:45
Salut.
Remarquons que :
(a^2+b^2+c^2-ab-bc-ca)+3abc)
fixons
en développant, ordonnant, on obtient :
(b+c+3bc+1)=r-1)
montrons que tout rationnel
peut s'écrire sous la forme de
(b+c+3bc+1))
posons
=\frac{t}{k})
soit
k - t=0)
^2 + 4t = m^2)
(
)
soit
(\frac{m}{2}+\frac{3bc+1}{2}))
il suffit de prendre :
(
)
soit
b= h-\frac{t}{h})
soit=0)
^2 + 12(\frac{t}{h}+1-h) = a^2)
(
)
en posant)
,
(a+3k))
il suffit de prendre :
ce qui est possible car on aucune condition sur
et que la fonction =x-\frac{C}{x})
est cool.
Remarquons que :
fixons
en développant, ordonnant, on obtient :
montrons que tout rationnel
posons
soit
soit
il suffit de prendre :
(
soit
soit
(
en posant
il suffit de prendre :
ce qui est possible car on aucune condition sur
par _-Gaara-_ » 02 Jan 2009, 14:02
Zweig a écrit:Ah, tiens je ne le connaissais pas ce poly ! Tu l'as trouvé comment ? Car le seul poly que j'ai sur les stratégies de base c'est un truc tout simple, celui-là est vachement développé !
c'est ça la prépa :zen:
par Zweig » 02 Jan 2009, 14:05
_-Gaara-_ a écrit:c'est ça la prépa :zen:
Rapport ? :hein:
Lapras, c'est bien compliqué tout ça, j'vais manger et je regarderais dans le détail plus tard.
par ThSQ » 02 Jan 2009, 14:48
Quid si on impose aux rationnels d'être > 0 (et le nombre aussi) ?
acoustica, il y a surement des personnes capables de deviner ça (quand on voit les formules de Ramanujan on se dit que tout est possible).
En général on trouve ce genre d'horreurs en cherchant des solutions d'une forme donnée.
Par exemple on cherche une solution a^3 + b^3 +c^3 avec a = u+v, b = u-v, c= fonction simple(u,v)
acoustica, il y a surement des personnes capables de deviner ça (quand on voit les formules de Ramanujan on se dit que tout est possible).
En général on trouve ce genre d'horreurs en cherchant des solutions d'une forme donnée.
Par exemple on cherche une solution a^3 + b^3 +c^3 avec a = u+v, b = u-v, c= fonction simple(u,v)
par lapras » 02 Jan 2009, 16:51
Bon j'en ai marre de chercher, je ne pense pas qu'il y ait de solution simple sans factorisation explicite...
par Zweig » 02 Jan 2009, 17:15
Bon, je propose ma solution. Soient 
et des rationnels, )
, )
, )
des fonctions à coefficients rationnels. On cherche des expressions de , 
, 
et 
vérifiant :  + v^3(r) = w^3(r) + rt)
On pose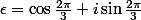
. Nous disposons de la factorisation suivante :
 + v^3(r) = [u(r) + v(r)][u(r)+\epsilon v(r)][u(r) + \epsilon^2v(r)])
On résout le système suivant, en terme de et :
 + \epsilon v(r) = (r-\epsilon)^3)
 + \epsilon^2v(r) = (r-\epsilon^2)^3)
Et on en tire l'identité suivante :
^{3}+\left(\frac{3r^{2}+3r}{r^{2}+r+1}\right)^{3}+(r-1)^{3}=9r)
Il ne reste plus qu'à diviser par 9.
On pose
On résout le système suivant, en terme de
Et on en tire l'identité suivante :
Il ne reste plus qu'à diviser par 9.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :