Ecriture d'un rationnel
Olympiades mathématiques, énigmes et défis
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 24 Déc 2008, 10:08
par acoustica » 24 Déc 2008, 10:08
Bonjour,
Un exo rigolo:
Montrer que pour tout nombre rationnel
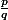
> 0, où q est un entier

1, il existe une unique famille dentiers {k,a1,...,ak},
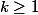
,
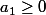
,

,

, pour tout entier i s'il en existe, tel que:

, telle que:
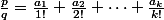
Joyeux noël et bon réveillon! :happy2:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Déc 2008, 14:57
par lapras » 24 Déc 2008, 14:57
Sauf erreur, ca se montre avec une suite de divisions euclidienne, avec une méthode similaire à celles d'une base quelconque.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 24 Déc 2008, 14:58
par acoustica » 24 Déc 2008, 14:58
lapras a écrit:Sauf erreur, ca se montre avec une suite de divisions euclidienne, avec une méthode similaire à celles d'une base quelconque.
Ouai mais c'est quand même pas si facile ^^
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Déc 2008, 15:01
par lapras » 24 Déc 2008, 15:01
J'ai pas trop le temps là mais avec un algo de divisions euclidiennes ca se fait bien.
J'écrirai ma solution plus tard.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Déc 2008, 18:16
par ThSQ » 24 Déc 2008, 18:16
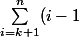/i! < (k-1)/k!)
donc pour construire la suite il suffit de prendre le

, qui existe forcément, tel que
/k!)
L'unicité en découle aussi.
Le processus se termine sinon le nombre obtenu ne serait pas rationnel (démo comme pour l'irrationalité de
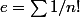
)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 25 Déc 2008, 13:42
par acoustica » 25 Déc 2008, 13:42
OK

ThSQ a écrit:Le processus se termine sinon le nombre obtenu ne serait pas rationnel (démo comme pour l'irrationalité de
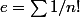
)
Ca m'interesse, tu m'expliques ça?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 25 Déc 2008, 17:26
par ThSQ » 25 Déc 2008, 17:26
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités