Dés truqués

[ComeDuRondeau]

Hello,

Je suis tombé sur un joli exercice qui j'espère vous plaira autant qu'il m'a plu !

Une menuisière souhaite tailler deux dés à faces numérotés de à . Elle aimerait piper les dés de telle sorte que le résultat de la somme suive une loi uniforme sur (on ne demande pas que les dés soient pipés de la même façon). Ce projet est-il réalisable ? Si oui décrire les lois possibles pour chacun des dés.

[Ben314]

Salut,
C'est un grand classique très connu et il y a de nombreuse preuves plus ou moins élaborées et, parmi les plus basiques, il y a celle là :
On note les probas des faces du premier dés et celle du deuxième.
Si les proba. le faire une somme de 2 et une somme de 12 sont les mêmes : alors

Donc la proba d'avoir une somme de 7 est au moins le double de .

Et si tu veut des variantes de ce problème, tu peut en trouver là :
enigmes/des-pipes-t102300.html

[ComeDuRondeau]

Chouette réponse ! J'avais celle de ffpower dans le lien que tu as cité. Elles ont l'air chouettes aussi les variantes. Pour mes étudiant.es j'ai rajouté comme question : on considère désormais qu'un dé est normal et l'autre a 7 faces (numéroté de 1 à 7), peut-on truquer le dé à 7 faces pour que la somme soit de loi uniforme ? Si oui quelle forme aura ce dé truqué ?

[lyceen95]

Une pièce de monnaie.
Extension amusante de ce problème classique.

[ComeDuRondeau]

Exact !!

On retrouve la façon "naturelle" qu'on ferait si on souhaitait créer une uniforme sur avec un dé et une pièce ; on jette le dé et la pièce et, en cas de face, on garde le résultat du dé, en cas de pile on ajoute 6 au résultat du dé.
(comme je l'ai énoncé ce serait plutôt on ajoute 1 en cas de face et 7 en cas de pile puisque je demande une uniforme sur mais c'est plus naturel comme présenté ci-dessus).

[Ben314]

Concernant les pièces et les dés, il y un truc assez marrant et classique :
Avec un copain, vous voulez jouer à un jeu de société qui nécessite un dés (à 6 faces, équilibré).
Sauf que, pas de bol, la dernière fois que votre fiston à joué au jeu (dehors et dans l'herbe bien sûr...), il a paumé le dés qu'il y avait dans la boite. Bref, vous avez plus de dés . . .
Le copain propose : et si on utilisait une pièce à la place du dés ?
Oui, mais comment procéder avec une simple pièce pour simuler un dés ?

[ComeDuRondeau]

Intuitivement je dirais qu'on fait 3 lancers de pièces et qu'on compte
Nombre de piles + 2*(Nombre de faces)
C'est ça ?

[Ben314]

Non, ça ne peut pas être exactement ça vu que, si tu ne jette qu'un nombre fini et constant de fois la pièce, le nombre de cas (équiprobables) ça va être et, quelque soit les "cas favorables", le ratio "cas favorable" / "cas total" ne pourra jamais être égale à 1/6 vu que 6 ne divise jamais .

Donc ton truc donne peut-être quelque chose d'approximativement correct (à voir...), mais surement pas une solution exacte.
Pour avoir un truc exact, il faut forcément un protocole où le nombre de lancé de la pièce est variable.
La solution simple (mathématiquement parlant) que je connais et quand même un peu chiante à utiliser dans un cas pratique . . .

[catamat]

Bonjour

Je ne pense pas que ce soit la solution de Ben314 mais il me semble que cela pourrait marcher :
On lance trois pièces
si on a trois fois le même résultat on recommence
sinon on a 6 issues possibles que l'on attribue aux six faces du dé (par ex : FFP=1,etc...)

Donc pour calculer la proba d'obtenir 1
On fait FFP au premier coup proba 1/8
On doit rejouer puis on fait FFP proba 1/4*1/8
On doit rejouer deux fois puis FFP proba (1/4)²*1/8
etc...
Donc

[Ben314]

Nickel : ça marche parfaitement
Et la preuve que ça marche est plutôt plus courte qu'avec la méthode que j'aurais employée :
On jette la pièce un certain nombre de fois jusqu’à ce que deux lancer successifs donnent le même résultat.
Si les deux derniers lancés (égaux) sont les mêmes que le premier, on compte 1 si c'est des Piles et 3 si c'est des Faces. Dans les autres cas, on compte 2 :
PP, PFPP, PFPFPP , . . .=>1 ; PFF, FPP, PFPFF, FPFPP , . . . => 2 ; FF, FPFF, FPFPFF , . . . => 3
On jette une fois de plus la pièce et on ajoute 3 au nombre si elle tombe sur Face.

Les méthodes sont-elles équivalentes en terme de "coût" : combien de fois, en moyenne, faut-il lancer la pièce pour avoir le résultat avec la méthode de catamat ? Et avec celle ci dessus ?

Et sinon, la méthode de catamat s'adapte parfaitement à toute simulation où les résultat qu'on veut simuler ont des proba. rationnelles : on calcule le ppcm M des dénominateurs des fractions (ici c'est 6), on jette N fois la pièce avec 2^N>=M (donc ici N=3) et si le résultat ne fait pas parti de M cas définis à l'avance (sur les 2^N), on réitère le jet de N pièces.
Mais peut-on, avec notre pièce, simuler un résultat style Gagné/Perdu tel que p(Gagné)=1/racine(2) par exemple ?

[catamat]

Je pensais en effet que cela marchait et je vois que se généralise même. Merci Ben314.
Personnellement je m'étais inspiré de la méthode pour jouer à pile ou face avec trois personnes (un exercice je pense assez classique)

Pour ce qui est du "coût" dans la méthode que j'ai proposé on jette des triplets de pièces avec chaque fois la proba p=3/4 de "succès" c'est à dire d'avoir un résultat.
La loi du premier succès est une loi géométrique de moyenne 1/p soit 4/3
Donc en moyenne 4/3 de triplet soit 4 pièces.

[catamat]

Si je ne me suis pas trompé dans mes calculs, par votre méthode Ben314 la moyenne est aussi de 4 je détaillerais plus tard (pas le temps en ce moment...)

[Ben314]

Oui, c'est effectivement aussi 4 jets de pièce en moyenne avec l'autre méthode ce qui donne l'impression que c'est deux fois la même chose. Sauf que l'éventuelle bijection entre les deux ne me saute (vraiment) pas aux yeux . . .

EDIT : si bijection il y a, elle est sans doute assez bizarre vu qu'avec ta méthode, le nombre de jeté de pièce est forcément un multiple de 3 alors qu'avec l'autre ça peut être n'importe quel entier .

Sinon, pour la proba de 1/racine(2), si personne ne s'y oppose, je mettrais la solution demain pour compléter le fil.

[catamat]

Bon finalement j'ai eu le temps de détailer :
Soit X le nombre de pièces à lancer avant d'avoir FF ou PP
Soit n supérieur ou égal à 2
Calculons p(X=n)
La première piéce est quelconque, ensuite les 2ème , 3ème etc jusqu'à la n-1 ème doivent être différentes de la précédente donc 1/2 à chaque fois et la nème doit être identique à la précédente donc encore 1/2
On a donc p(X=n)=(1/2)^(n-1)



Or
donc

en modifiant l'indice de départ

finalement


Mais comme on lance une dernière fois la pièce après avoir eu un doublon cela fait, semble t il, un "coût " de 4 jets.

[Ben314]

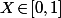
Pour simuler avec une pièce une épreuve de Bernoulli de proba. de réussite absolument quelconque la méthode théorique est on ne peut plus simple : on jette une infinité de fois la pièce, on note avec des 0 et des 1 la suite des résultats et on considère cette suite comme celle de l'écriture en base d'un réel . 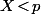La loi de est évidement la loi uniforme sur et, concernant la Bernoulli à simuler, il suffit bien sûr de dire que "Réussite" <=> pour avoir la bonne simulation.
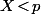
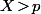
Bon, évidement, on peut se dire que ça va être un peu chaud de jeter une infinité de fois la pièce, mais en fait, non vu qu'on peut s’arrêter dés que les digits de (en base 2) déjà obtenues sont suffisant pour être sûr que ou bien que (par contre, le petit problème, c'est qu'il faut avoir l'écriture de en base 2 et que, si n'est pas rationnel, ça va pas être périodique)

Par exemple, pour simuler une épreuve de Bernoulli de proba de 1/3, on écrit 1/3 en base 2 :
1/3 = 0,010101010101... et donc on jette la pièce jusqu'au premier lancé ou la série de résultats obtenus diffère du début de la série 01010101... et on dit que la Bernoulli a réussi si la série obtenue correspond à l'écriture en base 2 d'un réel <1/3 donc ici, à condition d'avoir tiré 00 ou bien 01010...100 avec deux zéros à la fin. Par contre, si la série commence par 1 ou bien est de la forme 01010...1011 avec deux 1 à la fin, c'est "echec".
Et c'est avec cette méthode que j'ai "pondu" ma méthode consistant à attendre la première apparition de deux tirages identiques pour simuler un dés à 6 faces.