Salut,
Au cas ou tout le monde ne connaisse pas les quatres questions, un grand "classique" de proba. (tout un chacun peut rajouter des questions...) :
Tout le monde sait que, l'on jette deux dés "normaux" (i.e. sur chaque dé, les façes sont numérotées de 1 à 6 et sont équiprobables), les différentes sommes possibles ne sont pas équiprobables.
a) Peut-on, en utilisant deux dés "pipés'' (i.e. dont les faces ne sont pas équiprobables) et éventuellement différents, rendre les différentes sommes équiprobables ?
b) Est-il possible avec deux dés "pipés'' d'obtenir, pour les différentes sommes, les mêmes probabilités que celles que l'on a avec des dés "normaux" ?
c) Est-il possible, en changeant les nombres inscrits sur les faces des deux dés (mais en gardant des faces équiprobables) d'obtenir, pour les différentes sommes, les mêmes probabilités que celles que l'on a avec des dés "normaux" ?
d) Est-il possible, en changeant les nombres inscrits sur les faces des deux dés ET en pipant les dés d'obtenir avec équiprobabilité les sommes 2,3,4,...,12 ?
P.S. Pour la c) et la d), les nombres inscrits sur les faces ne sont pas forcément entiers, pas forcément différents sur deux faces différentes, et pas forcément les mêmes sur les deux dés...
Dés pipés
6 messages
- Page 1 sur 1
Pour la a)
Je note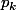 (resp
(resp 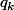 ) la probabilité d'obtenir k avec le 1er dé(resp 2eme dé), et si je note
) la probabilité d'obtenir k avec le 1er dé(resp 2eme dé), et si je note =\sum_{k=0}^6p_{k+1}x^k) et
et =\sum_{k=0}^6q_{k+1}x^k) , alors on doit avoir
, alors on doit avoir Q(x)=\frac{1}{11}(1+x+x^2+^\cdots+x^10)) . Or ce dernier polynome n'a comme racine que des complexes ( les racines 11-iemes de l'unités différentes de 1). Mais P et Q étant réels de degré impair, ils sont censés avoir au moins une racine réelle. Donc c'est pas possible..
. Or ce dernier polynome n'a comme racine que des complexes ( les racines 11-iemes de l'unités différentes de 1). Mais P et Q étant réels de degré impair, ils sont censés avoir au moins une racine réelle. Donc c'est pas possible..
Voila, j'ai envie d'utiliser le même genre d'idées pour les questions d'après, mais j'y ai pas encore réfléchi..
Je note
Voila, j'ai envie d'utiliser le même genre d'idées pour les questions d'après, mais j'y ai pas encore réfléchi..
Bonne réponse et... bonne méthode pour le a) et le b)...
Pour le c) et le d) je ne connais pas de "jolie preuve", c'est à dire ne nécéssitant pas un minimum de "tests"... (ce qui ne prouve bien évidement pas que de telles méthodes n'existent pas...)
Pour le c) et le d) je ne connais pas de "jolie preuve", c'est à dire ne nécéssitant pas un minimum de "tests"... (ce qui ne prouve bien évidement pas que de telles méthodes n'existent pas...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour,
pour le a) j'avais une méthode peut-être plus directe que de passer par R[X] : on a
 et
et  , donc :
, donc :
)
 (propriété de la fonction x+1/x)
(propriété de la fonction x+1/x)
La probabilité d'obtenir "7", qui vaut la somme des p_i q_{7-i} est donc sup. ou égale au membre de gauche de l'inégalité, lui-même strictement sup. à 1/11. Donc il est impossible de simuler l'équiprobabilité des résultats.
Cette démonstration permet aussi de sentir les choses : pour assurer l'équiprobabilité des résultats 2 et 12 il faut mettre un poids très fort sur les faces 1 et 6 des dés, ce qui déséquilibre les autres résultats ...
pour le a) j'avais une méthode peut-être plus directe que de passer par R[X] : on a
La probabilité d'obtenir "7", qui vaut la somme des p_i q_{7-i} est donc sup. ou égale au membre de gauche de l'inégalité, lui-même strictement sup. à 1/11. Donc il est impossible de simuler l'équiprobabilité des résultats.
Cette démonstration permet aussi de sentir les choses : pour assurer l'équiprobabilité des résultats 2 et 12 il faut mettre un poids très fort sur les faces 1 et 6 des dés, ce qui déséquilibre les autres résultats ...
Re: Dés pipés
Je tente ma chance pour les b), c) et d) puisqu'il n'y a pas encore de réponses !
On note et
et  les variables aléatoires représentant chacun des dés de fonctions génératrices
les variables aléatoires représentant chacun des dés de fonctions génératrices =\sum_{k=1}^6 p_k t^k=tP_X(t)) avec
avec 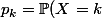) et
et =tP_Y(t)) définie de la même manière. De la même façon que ffpower on devrait avoir
définie de la même manière. De la même façon que ffpower on devrait avoir 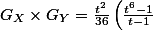^2) ce qui revient à
ce qui revient à 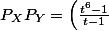^2) .
.
Or on sait factoriser^2) en facteurs irréductible dans
en facteurs irréductible dans  :
:
^2=(t+1)^2(t^2+t+1)^2(t^2-t+1)^2) .
.
Les seuls facteurs de degré 5 sont
*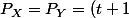(t^2+t+1)(t^2-t+1)) ce qui correspond à X et Y qui sont des dés équilibrés
ce qui correspond à X et Y qui sont des dés équilibrés
*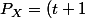(t^2+t+1)^2) et
et 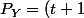(t^2-t+1)^2) mais ce dernier n'est pas à coefficients positifs donc ne définit pas une fonction génératrice de variable aléatoire
mais ce dernier n'est pas à coefficients positifs donc ne définit pas une fonction génératrice de variable aléatoire
* (le cas symétrique au précédent)
Donc non on ne peut pas avoir une somme de dés pipés qui se comporte comme une somme de dés équilibrés !
Une possibilité serait de choisir n'importe quel dans
dans  et de considérer un dé dont les faces sont
et de considérer un dé dont les faces sont  et l'autre
et l'autre  . Je pensais qu'il s'agissait de la seule solution mais en essayant de le prouver j'en ai trouvé d'autres.
. Je pensais qu'il s'agissait de la seule solution mais en essayant de le prouver j'en ai trouvé d'autres.
Si on note les numéros sur le premier dé et
les numéros sur le premier dé et  ceux sur le second rangés dans l'ordre strictement croissant avec
ceux sur le second rangés dans l'ordre strictement croissant avec  alors, en notant
alors, en notant  , puisqu'on doit avoir
, puisqu'on doit avoir  . De plus
. De plus  donc
donc  avec
avec  entier et, de la même façon
entier et, de la même façon  avec
avec  entier et
entier et  avec
avec  entier.
entier.
Donc et
et  , on est donc ramené au problème où les réels sur les faces sont des entiers naturels et on peut alors utiliser les fonctions génératrices comme au dessus pour conclure.
, on est donc ramené au problème où les réels sur les faces sont des entiers naturels et on peut alors utiliser les fonctions génératrices comme au dessus pour conclure.
Il s’agit de factoriser^2) en deux polynômes mais sans la restriction que les facteurs soient de degré
en deux polynômes mais sans la restriction que les facteurs soient de degré  . Les seules restrictions sont que les facteurs soient à coefficients positifs et qu’ils aient moins de
. Les seules restrictions sont que les facteurs soient à coefficients positifs et qu’ils aient moins de  coefficients (car le dés a toujours
coefficients (car le dés a toujours  faces). Quelques boucles en python donnent trois solutions :
faces). Quelques boucles en python donnent trois solutions :
*=\frac{t}{4}\left(t^2+2t+1\right)) et
et =\frac{t}{9}\left(t^8+2t^6+3t^4+2t^2+1\right)) (donc un premier dé avec pour numéros 3 avec proba
(donc un premier dé avec pour numéros 3 avec proba 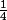 , 2 avec proba
, 2 avec proba et 1 avec proba
et 1 avec proba 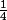 et l'autre avec pour numéros 9 avec proba
et l'autre avec pour numéros 9 avec proba 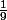 , 7 avec proba
, 7 avec proba  , 5 avec proba
, 5 avec proba 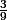 , 3 avec proba
, 3 avec proba  , 1 avec proba
, 1 avec proba 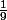 .
.
*=\frac{t}{6}\left(t^3+2t^2+2t+1\right)) et
et =\frac{t}{6}\left(t^7+t^5+t^4+t^3+t^2+1\right)) (il me semble que c’est la seule solution pouvant être réalisée avec des dés équilibrés, le premier aurait sur ses faces
(il me semble que c’est la seule solution pouvant être réalisée avec des dés équilibrés, le premier aurait sur ses faces  et le second
et le second  ).
).
*=\frac{t}{9}\left(t^4+2t^3+3t^2+2t+1\right)) et
et =\frac{t}{4}\left(t^6+2t^3+1\right))
Donc trois solutions !
De la même que pour la réponse à la variante c) on se ramène au cas où les numéros sur les dés sont des entiers naturels supérieurs à (à un
(à un  réel près...). Toujours avec les fonctions génératrices il s'agit maintenant de factoriser
réel près...). Toujours avec les fonctions génératrices il s'agit maintenant de factoriser ) en un produit de deux polynômes réels à coefficients positifs et ayant moins de
en un produit de deux polynômes réels à coefficients positifs et ayant moins de  coefficients non nuls. On sait factoriser
coefficients non nuls. On sait factoriser ) en facteurs réels irréductible qui sont les
en facteurs réels irréductible qui sont les =t^2-2\cos\left(\frac{2k\pi}{11}\right)t+1) pour
pour  allant de 1 à 5. Or encore une petite boucle en Python nous apprend que le produit de 3
allant de 1 à 5. Or encore une petite boucle en Python nous apprend que le produit de 3 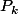 a toujours
a toujours  coefficients non nuls et le produit de 4
coefficients non nuls et le produit de 4 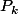 en a toujours
en a toujours  donc impossible de représenter des lois de dés à 6 faces.
donc impossible de représenter des lois de dés à 6 faces.
Ben314 a écrit:b) Est-il possible avec deux dés "pipés'' d'obtenir, pour les différentes sommes, les mêmes probabilités que celles que l'on a avec des dés "normaux" ?
On note
Or on sait factoriser
Les seuls facteurs de degré 5 sont
*
*
* (le cas symétrique au précédent)
Donc non on ne peut pas avoir une somme de dés pipés qui se comporte comme une somme de dés équilibrés !
Ben314 a écrit:c) Est-il possible, en changeant les nombres inscrits sur les faces des deux dés (mais en gardant des faces équiprobables) d'obtenir, pour les différentes sommes, les mêmes probabilités que celles que l'on a avec des dés "normaux" ?
Une possibilité serait de choisir n'importe quel
Si on note
Donc
Il s’agit de factoriser
*
*
*
Donc trois solutions !
d) Est-il possible, en changeant les nombres inscrits sur les faces des deux dés ET en pipant les dés d'obtenir avec équiprobabilité les sommes 2,3,4,...,12 ?
De la même que pour la réponse à la variante c) on se ramène au cas où les numéros sur les dés sont des entiers naturels supérieurs à
Re: Dés pipés
Depuis le temps (2010...), j'ai évidement complètement paumé mes propres solutions, mais en lisant les tiennes, tout me semble parfaitement correct et il me semble que c'est bien ce que j'avais trouvé dans le temps : en particulier, les fameux deux dés (1,2,2,3,3,4) et (1,3,4,5,6,8) qui donnent la même somme que les dés normaux.
Donc . . . BRAVO !!!
Donc . . . BRAVO !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
