2) Des triplets
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 13 Jan 2007, 13:01
par nekros » 13 Jan 2007, 13:01
Salut :we:
Montrer qu'il n'existe qu'un
nombre fini de triplets
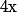
,
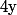
,
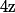
d'entiers naturels tels que :
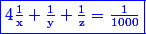
Bonne réflexion...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Jan 2007, 13:20
par fahr451 » 13 Jan 2007, 13:20
l'application f(x,y,z) = (1/1000)xyz-xy-yz-zy définie sur [1,+inf [^3
tend vers +infini qd ll(x,y,z)llinf tend vers +inf donc hors d'un certain disque
f est strictement positive. les solutions de f(x,y,z) = 0 sont à rechercher ds le disque et un nbre fini pour de triplets entiers
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 13 Jan 2007, 18:59
par Imod » 13 Jan 2007, 18:59
Une première idée ( sans aucunes vérifications ) on peut supposer sans changer la "finitude" du nombre de solutions que
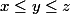
.
Si
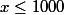
alors
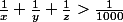
impossible .
Si
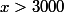
alors
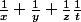
: impossible .
Si y>2t alors
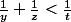
: impossible .
Alors x , y et z sont dans des intervalles bornés et le nombre de solutions est fini .
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités