Des carrés magiques : un problème vieux de plus de 200 ans
Des carrés magiques : un problème vieux de plus de 200 ans
"Christian Boyer, amateur de carrés magiques, propose de régler un problème vieux de plus de 200 ans en stimulant les matheux par des prix (8000 ) et des bouteilles de champagne (12) pour une résolution de 12 énigmes. Le détail des énigmes quil propose se trouve chez lui. Il sagit pour lessentiel de prouver quil est possible (ou pas) de construire un carré de 3 lignes et 3 colonnes dont chaque entier est un entier au carré. En fait C.B. met à prix 6 énigmes plus ou moins liées à ce problème afin dapprocher sa résolution" (l'extrait provient d'article de 2010 de Science et Avenir encore d'actualité).
Deliantha a écrit:"Christian Boyer, amateur de carrés magiques, propose de régler un problème vieux de plus de 200 ans en stimulant les matheux par des prix (8000 ) et des bouteilles de champagne (12) pour une résolution de 12 énigmes. Le détail des énigmes quil propose se trouve chez lui. Il sagit pour lessentiel de prouver quil est possible (ou pas) de construire un carré de 3 lignes et 3 colonnes dont chaque entier est un entier au carré. En fait C.B. met à prix 6 énigmes plus ou moins liées à ce problème afin dapprocher sa résolution" (l'extrait provient d'article de 2010 de Science et Avenir encore d'actualité).
En voilà un
13² 7² 17²
17² 13² 7²
7² 17² 13²
On en trouve rapidement d'autres. C'est trop facile, il doit manquer un truc dans le texte
chan79 a écrit:ah, ça dépend, c'est une question de définition
jamis vu utiliser le mème nombre dans les carrés magiques, sinon avec du
111
111
111
on a de superpropriétés!
maintenant les trucs où Boyer ne sait pas faire,
faut de bonnes bases
ou un bon ordinateur
ou les deux!
"Christian Boyer, amateur de carrés magiques"
c'est plutot Boyer professionnel en carrés magiques"!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:jamis vu utiliser le mème nombre dans les carrés magiques, sinon avec du
111
111
111
on a de superpropriétés!
maintenant les trucs où Boyer ne sait pas faire,
faut de bonnes bases
ou un bon ordinateur
ou les deux!
"Christian Boyer, amateur de carrés magiques"
c'est plutot Boyer professionnel en carrés magiques"!
Evidemment qu'on ne va pas trouver comme ça quelque chose que des gens bien plus malins n'ont pas trouvé depuis des années.
Il y a quand même des études qui ont été faites sur des carrés "magiques" avec des nombres qui se répètent. Tiens, il y a celui de la Sagrada Familia
[img][IMG]http://img13.imageshack.us/img13/5189/sagradanum.jpg[/img][/IMG]
Il y a en effet un souci de définition; tout le monde n'est pas d'accord avec le principe de base.
Pour certains, le carré magique d'ordre n contient tous les nombre de 1 à n^2. Donc, sans répétition ou omission. Pour d'autre, un carré magique contient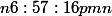 nombres entiers qui peuvent être ou non distincts.
nombres entiers qui peuvent être ou non distincts.
Donc, le problème #1 : "carré magique 3x3 utilisant 7 entiers carrés distincts"
Siginifie très clairement que :
- les 9 éléments du carré (3x3) sont tous des entiers élevés au carré
- il n'y a "que" 7 entiers distincts, donc clairement trois ou deux fois deux éléments doivent être identiques.
Appelons n1, n2, ..., n7 les sept entiers distincts.
Le caré 3x3 se compose des 9 éléments d'un des deux ensembles suivants
{n1, n1, n1, n2, n3, n4, n5, n6, n7} ou {n1, n1, n2, n2, n3, n4, n5, n6, n7}
Je ne vois pas d'autre façon de construire un ensemble de neuf entiers avec 7 distincts.
L'exemple ci-dessus de la strada familia est un bon exemple d'un carré 4x4 avec 14 entiers distincts.
Pour certains, le carré magique d'ordre n contient tous les nombre de 1 à n^2. Donc, sans répétition ou omission. Pour d'autre, un carré magique contient
Donc, le problème #1 : "carré magique 3x3 utilisant 7 entiers carrés distincts"
Siginifie très clairement que :
- les 9 éléments du carré (3x3) sont tous des entiers élevés au carré
- il n'y a "que" 7 entiers distincts, donc clairement trois ou deux fois deux éléments doivent être identiques.
Appelons n1, n2, ..., n7 les sept entiers distincts.
Le caré 3x3 se compose des 9 éléments d'un des deux ensembles suivants
{n1, n1, n1, n2, n3, n4, n5, n6, n7} ou {n1, n1, n2, n2, n3, n4, n5, n6, n7}
Je ne vois pas d'autre façon de construire un ensemble de neuf entiers avec 7 distincts.
L'exemple ci-dessus de la strada familia est un bon exemple d'un carré 4x4 avec 14 entiers distincts.
Les carrés magiques à la base se remplissent avec les nombres de 1 à n^2.
Somme constante sur les rangées, les colonnes et les 2 diagonales.
Et cela concerne l'addition en puissance de 1.
Les différentes propriétés avec les diagos viennent donner des noms comme panmagiques, diaboliques.
Ensuite il y a la mème chose avec les cubes.
Si mes souvenirs sont bons Boyer avec un collègue allemand? a été le premier à trouver un cube de 5 avec les diagonales sur les carrés et les diagonales du cube.
Comme on peut inscrire des messages codés, on peut aussi acepter des versions "dégradées" avec des nombres différents,comme Sagrada Familia.
Boyer a aussi beaucoup bossé les carrés magiques où on additionne les carrés des nombres, voire d'autres puissances.C'est un domaine que je n'ai jamais exploré.
mais on conçoit alors que les nombres peuvent ètre non consécutifs de 1 à n^2,
voire oblige à des répétitions comme le 3x3 avec 7 distincts.
Ok, ça baigne alors!
Somme constante sur les rangées, les colonnes et les 2 diagonales.
Et cela concerne l'addition en puissance de 1.
Les différentes propriétés avec les diagos viennent donner des noms comme panmagiques, diaboliques.
Ensuite il y a la mème chose avec les cubes.
Si mes souvenirs sont bons Boyer avec un collègue allemand? a été le premier à trouver un cube de 5 avec les diagonales sur les carrés et les diagonales du cube.
Comme on peut inscrire des messages codés, on peut aussi acepter des versions "dégradées" avec des nombres différents,comme Sagrada Familia.
Boyer a aussi beaucoup bossé les carrés magiques où on additionne les carrés des nombres, voire d'autres puissances.C'est un domaine que je n'ai jamais exploré.
mais on conçoit alors que les nombres peuvent ètre non consécutifs de 1 à n^2,
voire oblige à des répétitions comme le 3x3 avec 7 distincts.
Ok, ça baigne alors!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Effectivement, mais le dénombrement n'est pas évident. J'ai toujours beaucoup de mal avec les cube et les carré car leur grand nombre de symétrie a vite fait de m'embrouiller.
Quoique là en l'occurence, toutes les permutations de lignes et colonnes ne sont pas possible car il faut conserver les diagonales !
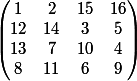
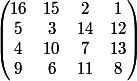
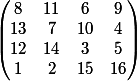
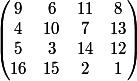
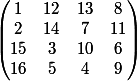
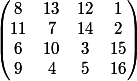
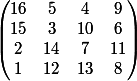
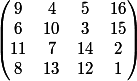
Quoique là en l'occurence, toutes les permutations de lignes et colonnes ne sont pas possible car il faut conserver les diagonales !
beagle a écrit:euh oui, la démonstration du nombre relève de la pensée magique,
mais 880 est le bon nombre car c'est pas moi qui l'ai trouvé!
Tu crois peut-être que l'on avait pas vu l'arnaque....
Mais ca doit être pas être compliqué de le programmer
- vu le peu de profondeur on peut attaquer par une fonction récursive,
- il faut réfléchir un peu pour éliminer les identiques par rotation & symétrie
- et il y a certainement un ordre pour remplir les cases qui réduit le nombre de tests
Et comme dit Beagle à la fin ca affiche : 880 solutions !
"Tu crois peut-être que l'on avait pas vu l'arnaque...."
Si une ou deux personnes ont pu croire un instant que j'avais un don cela me suffit pour cette journée.
Et c'est un pote à toi qui a dénombré ça (le premier?):
"Frenicle a montré qu'il y avait 880 carrés magiques d'ordre 4."
Gérard Villemin
Frenicle c'est bien lui qui envoyait des mails à Fermat sur le fil fabriquer un carré ...
Si une ou deux personnes ont pu croire un instant que j'avais un don cela me suffit pour cette journée.
Et c'est un pote à toi qui a dénombré ça (le premier?):
"Frenicle a montré qu'il y avait 880 carrés magiques d'ordre 4."
Gérard Villemin
Frenicle c'est bien lui qui envoyait des mails à Fermat sur le fil fabriquer un carré ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:"Et c'est un pote à toi qui a dénombré ça (le premier?):
"Frenicle a montré qu'il y avait 880 carrés magiques d'ordre 4."
Gérard Villemin
Frenicle c'est bien lui qui envoyait des mails à Fermat sur le fil fabriquer un carré ...
On est d'accord c'est bien lui !!!
Sinon j'ai mis les 16 nombres dans la moulinette : sans test de rotation / symétrie, la machine recrache 7040 solutions
Et comme 880*8 =7040... on sent que c'est bien parti....
beaucoup de refs sur les carrés d'ordre 4 parlent de la classification de Dudeney,
mais j'ai pas retrouvé sur le net comment c'est-y qu'ils les a rangés.
par ordre croissant sue la première rangée de gauche à droite puis deuxième rangée and so on,
well don't know.
mais j'ai pas retrouvé sur le net comment c'est-y qu'ils les a rangés.
par ordre croissant sue la première rangée de gauche à droite puis deuxième rangée and so on,
well don't know.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
LeJeu a écrit:On est d'accord c'est bien lui !!!
Sinon j'ai mis les 16 nombres dans la moulinette : sans test de rotation / symétrie, la machine recrache 7040 solutions
Et comme 880*8 =7040... on sent que c'est bien parti....
Ma moulinette me donne aussi 7040
Si on considère comme un seul carré magique ceux qui se déduisent par certaines transformations, il faut diviser par 8 et on arrive bien à 880
beagle a écrit:"Et comme 880*8 =7040... on sent que c'est bien parti...."
Je vois bien que tu raisonnes comme moi finalement!
Pour éliminer les rotations
- on cherche tous les carrés avec un 1 en haut à gauche
- On cherche tous les carrés avec un 2 en haut à gauche et on rejette tous les carrés avec un 1 dans les trois autres coins
- On cherche tous les carrés avec un 3 en haut à gauche et on rejette tous les carrés avec un 1 ou un 2 dans les trois autres coins
....
et hop on a divisé par 4 le nombre de solutions !
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
