Défi : Une inégalité [Niveau : Supérieur]
Olympiades mathématiques, énigmes et défis
-
samoufar
- Membre Relatif
- Messages: 401
- Enregistré le: 28 Mai 2016, 17:43
- Localisation: Palaiseau
-
 par samoufar » 11 Sep 2016, 16:32
par samoufar » 11 Sep 2016, 16:32
Bonjour à toutes et à tous,Je vous propose un petit
défi (niveau
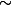
Bac+2) : montrer une inégalité.
Attention ça n'est pas aussi facile que ça en a l'air  Énoncé
ÉnoncéSoit
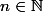
.
DéfinitionOn note
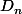
l'ensemble des éléments de
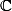
de module

dont une détermination

de l'argument vérifie
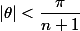
.
QuestionMontrer que pour tout élément

de
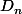
et tout

de
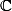
de module

n'appartenant pas à
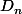
,
\cdot (z-\overline{\alpha})\vert\leq\vert 1-\alpha\vert ^2)
Bon courage à ceux qui relèvent le défi


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Sep 2016, 17:37
par zygomatique » 11 Sep 2016, 17:37
salut
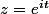
avec
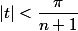
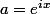
et posons
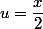
et
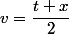
et
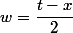
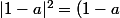(1 - \bar a) = (e^{-iu} - e^{iu})(e^{iu} - e^{-iu}) = 4 |\sin \frac x 2|)
(e^{it} - e^{-ix}) = e^{iv}(e^{i(v + w)} - e^{i(v - w)})e^{iw}(e^{i(w + v)} - e^{i(w - v)}))
ouais bof faut voir si on arrive à obtenir le module simplement ... sinon passer en mode trigo puis formulaire ...
to be continued ... plus tard ...

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
samoufar
- Membre Relatif
- Messages: 401
- Enregistré le: 28 Mai 2016, 17:43
- Localisation: Palaiseau
-
 par samoufar » 11 Sep 2016, 18:42
par samoufar » 11 Sep 2016, 18:42
zygomatique a écrit:(e^{it} - e^{-ix}) = e^{iv}(e^{i(v + w)} - e^{i(v - w)})e^{iw}(e^{i(w + v)} - e^{i(w - v)}))
Avec tes notations, ça serait plutôt
(e^{it} - e^{-ix}) = e^{iv}(e^{iw} - e^{-iw})e^{iw}(e^{iv} - e^{-iv}))
Autre chose, en remarquant le l'inégalité ne change pas si on remplace l'un ou l'autre des complexes par son conjugué, on peut s'arranger pour éliminer les valeurs absolues


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Sep 2016, 18:58
par zygomatique » 11 Sep 2016, 18:58
ha mais oui bien sur ... une erreur bête (comme toutes les erreurs ou presque !!)
je m'étonnais de ne pas trouver un truc du même genre que la ligne du dessus ...
je poursuivrais plus tard ...
merci
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
