Couples rationnels
Olympiades mathématiques, énigmes et défis
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 27 Aoû 2008, 20:15
par guigui51250 » 27 Aoû 2008, 20:15
leon1789 a écrit:Je ne comprends pas comment tu sais que p et q sont étrangers. Pourquoi le sont-ils ?
bah justement c'est cette phrase là qui me gène dans la correction du magazine donc peut-être que quelqu'un pourra lever le mystère ^^
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 27 Aoû 2008, 20:23
par Euler911 » 27 Aoû 2008, 20:23
Bonjour,
Quel est le numéro du magazine Tangente où tu as trouvé le problème?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 20:42
par leon1789 » 27 Aoû 2008, 20:42
guigui51250 a écrit:Le nombre
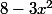
doit donc être le carré d'un rationnel et il existe des entiers p,q et a tels que
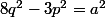
Ecrivons

et
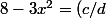^2)
.
Alors
^2 = (c/d)^2)
, donc

. Si on identifie, on obtient q=(fd), p=(ed), a=(cf). Personne n'est premier avec qui que se soit a priori... Si ? :hein:
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 27 Aoû 2008, 21:02
par guigui51250 » 27 Aoû 2008, 21:02
Euler911 a écrit:Bonjour,
Quel est le numéro du magazine Tangente où tu as trouvé le problème?
Hors série thématique de mai 2008
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 27 Aoû 2008, 21:03
par guigui51250 » 27 Aoû 2008, 21:03
leon1789 a écrit:Ecrivons

et
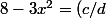^2)
.
Alors
^2 = (c/d)^2)
, donc

. Si on identifie, on obtient q=(fd), p=(ed), a=(cf). Personne n'est premier avec qui que se soit a priori... Si ? :hein:
ouè c'est bizarre ça me gène vraiment cette histoire de nombres premiers :hum:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Aoû 2008, 21:25
par Zweig » 27 Aoû 2008, 21:25
Autre méthode à l'aide de la descente infinie :
En reduisant l'équation modulo 8, si un triplet existe, alors il existe des entiers a' et p' vérifiant a = 8a' et p = 8p', a' < a, p < p'
etc ...
on retombe après sur une équation de la forme de départ etc ..

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:41
par leon1789 » 27 Aoû 2008, 22:41
Alors p et q doivent être multiple de 3 ce qui est
contradictoire avec le fait qu'ils soient premiers entre eux donc pas de solutions apars
)
Allez, je branche mon magnéto (...Serge)
>
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 27 Aoû 2008, 23:06
par Euler911 » 27 Aoû 2008, 23:06
leon1789 a écrit:Allez, je branche mon magnéto (...Serge)
>
Rolala mais qui à pu donc inventer la démonstration par l'absurde?! :doh: :hum:
Ok je sors...--->[]

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 23:08
par leon1789 » 27 Aoû 2008, 23:08
Euler911 a écrit:Rolala mais qui à pu donc inventer la démonstration par l'absurde?! :doh: :hum:
ben oui, on se le demande ! :ptdr:
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 28 Aoû 2008, 07:16
par guigui51250 » 28 Aoû 2008, 07:16
Enfait cette équation là elle ressemble un peu à du Bezout
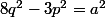
mais le problème c'est qu'elle ne fait qu'y ressemble je crois :briques:
C'est quand même bizarre qu'un magazine comme Tangente puisse se tromper :mur: il y a peut-être quelque chose qui nous a échappé :mur:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 29 Aoû 2008, 13:57
par Zweig » 29 Aoû 2008, 13:57
Si le triplet
)
est solution, alors le triplet
)
l'est aussi. On peut donc se ramener au cas où ces entiers sont positifs.
En réduisant modulo 3 l'équation considérée, on montre que

et

doivent être des multiples de 3,

et

avec

et

. L'équation devient, après simplification :

On montre de même que

est un multiple de 3,

avec

. L'équation devient alors :

La descente infinie est enclenchée ...
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 29 Aoû 2008, 14:15
par guigui51250 » 29 Aoû 2008, 14:15
Zweig a écrit:Si le triplet
)
est solution, alors le triplet
)
l'est aussi. On peut donc se ramener au cas où ces entiers sont positifs.
En réduisant modulo 3 l'équation considérée, on montre que

et

doivent être des multiples de 3,

et

avec

et

. L'équation devient, après simplification :

On montre de même que

est un multiple de 3,

avec

. L'équation devient alors :

La descente infinie est enclenchée ...
ouè mais comment expliques-tu que q et p soit premiers entre eux?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 29 Aoû 2008, 14:18
par Zweig » 29 Aoû 2008, 14:18
Ah vous êtes toujours sur ça, j'ai cru que vous étiez entrain de chercher une autre méthode :briques: Humm, bah je ne vois pas en quoi ces nombres sont premiers entre eux :help:
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 29 Aoû 2008, 15:46
par guigui51250 » 29 Aoû 2008, 15:46
Zweig a écrit:Ah vous êtes toujours sur ça, j'ai cru que vous étiez entrain de chercher une autre méthode :briques: Humm, bah je ne vois pas en quoi ces nombres sont premiers entre eux :help:
ouè parce que des solutions on en a trouvé plein mais c'est dans la solution de Tangente qu'il y a des nombres premiers mais personne ne sait pourquoi... mystère lol
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Aoû 2008, 16:17
par Doraki » 29 Aoû 2008, 16:17
L'équation étant homogène, pour tout k non nul et pour tous p,q, (p, q) est une solution <=> (kp,kq) est une solution. Donc autant décider de ne chercher que les solutions primitives qui ont pgcd(p,q)=1, parcequ'avec elles on peut retrouver toutes les autres après.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 29 Aoû 2008, 16:51
par Zweig » 29 Aoû 2008, 16:51
De quelle équation parles-tu ? Celle du topic ou celle de guigui ? Dans tous les cas, ces équations n'admettent aucune solution.
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 29 Aoû 2008, 16:55
par guigui51250 » 29 Aoû 2008, 16:55
Doraki a écrit:L'équation étant homogène, pour tout k non nul et pour tous p,q, (p, q) est une solution (kp,kq) est une solution. Donc autant décider de ne chercher que les solutions primitives qui ont pgcd(p,q)=1, parcequ'avec elles on peut retrouver touts les autres après.
bah ouè dans tous les cas il n'y a que le couple (0,0) qui est solution
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Aoû 2008, 17:13
par Doraki » 29 Aoû 2008, 17:13
ben peu importe, les deux le sont. C'était pour justifier le raisonnement (inutilement compliqué certes) qu'ils ont fait dans Tangente.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 29 Aoû 2008, 17:27
par leon1789 » 29 Aoû 2008, 17:27
Doraki a écrit:ben peu importe, les deux le sont. C'était pour justifier le raisonnement (inutilement compliqué certes) qu'ils ont fait dans Tangente.
Je ne vois pas en quoi cela explique leur binz car l'équation

est certes homogène, mais cela implique seulement que l'on peut supposer a,p,q premiers entre eux dans leur ensemble, pas deux à deux. Je me trompe ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Aoû 2008, 17:36
par Doraki » 29 Aoû 2008, 17:36
Ah ouais.
Ils ont vraiment écrit n'importe quoi en fait.
Il sont passés de 8-3x² = (p/q)² (là on peut dire p et q premiers entre eux)
soit 8q²-3(xq)² = p² (qui est bien homogène en p,q) à un truc où ils se gourrent de noms de variables et à cause de ça ça part en délire ils sont forcés de faire des trucs louches au lieu de dire directement 2q²=p² modulo 3. Ce qui implique bien q=p=0 mod 3 et contradiction.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
est solution, alors le triplet
l'est aussi. On peut donc se ramener au cas où ces entiers sont positifs.
et
doivent être des multiples de 3,
et
avec
et
. L'équation devient, après simplification :
est un multiple de 3,
avec
. L'équation devient alors :