Couples d'entiers

par **aviateurpilot** » 16 Juil 2006, 14:54

Trouver tous les couples d'entiers (x,y) tels que :

c'est mon dernier message
car je vais aller en vacance

par **calius** » 16 Juil 2006, 15:10

salut
l'expononciel de ton egalite donne (exp(2))^(3x+1)=exp(y²-1)
on la met en ln on a (3x+1)ln(2)=ln(y²-1)
evidement il fait tenir on compte du domaine de difinition de ln(y²-1)

par **nekros** » 16 Juil 2006, 15:28

Salut,

On peut poser

L'équation

devient donc

Les solutions sont donc

et

Ces solutions sont définies pour

(plus ou moins)

On a donc

et

Là encore, il faut faire attention à ce que ces solutions soient bien définies.

Reste à trouver les valeurs de

entier telles que x soit entier.

C'est la bonne piste ou pas ?

Thomas G :zen:

par **Mikou** » 16 Juil 2006, 15:31

lol non c'ets pas la bonne piste :p dans ce genre dexo il faut utiliser des regles simple de larithmetique en general :)

par **nekros** » 16 Juil 2006, 15:35

Par exemple, le couple (x=0,y=2) convient.

Thomas G :zen:

par **nekros** » 16 Juil 2006, 15:36

:ptdr: Bah ça marche quand même !

PS : J'ai jamais fait d'arithmétique
Je ne sais même pas ce qu'est une congruence !!

Thomas G :zen:

par **Mikou** » 16 Juil 2006, 15:40

mdr? pourtant les pb que tu pose ne sont pas simples ... c'est quoi ton niveau ?

par **nekros** » 16 Juil 2006, 15:43

J'ai terminé ma math spé en prépa option PC*
PS : pour les problèmes d'arithmétique, j'arrive toujours à trouver une combine, souvent un truc foireux mais qui donne le bon résultat :ptdr:

Thomas G :zen:

par **aviateurpilot** » 16 Juil 2006, 15:44

je reste avec vous encore ce jour avant les vacances :++:

par **nekros** » 16 Juil 2006, 15:48

Alors aviateurpilot, tu pars où ??

Thomas G :zen:

par **Mikou** » 16 Juil 2006, 15:58

ok nekros :p j'aurai cru qu'en pcsi on voyait qq th d'arithmétique ^^

par **aviateurpilot** » 16 Juil 2006, 16:00

à agadir

:zen:

par **aviateurpilot** » 16 Juil 2006, 16:24

on travaille dans N
ok

par **aviateurpilot** » 16 Juil 2006, 16:30

si x=0; y=2
si x>0

puisque y est impair.
alors

donc

et

(1)
ou

et

(2) (avec PGCD(a,b)=1 et a et b impair)
(1) donne

(2) donne

ma tete ne veus plus continuer :we:
car je ne pense à agadir :ptdr:
A+

par **BancH** » 16 Juil 2006, 21:20

On va chercher les valeurs d'unité que peut prendre

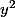
Les valeurs que peut prendre le chiffre des unités d'un nombre élevé au carré sont : 0,1,4,5,6,9.

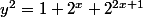
, l'expression

peut donc adopter comme chiffre des unités : 0,1,4,5,6 ou 9.

Si l'on cherche maintenant le chiffre des unité de

, on trouve : 0,3,4,5,8,9.

étant pair, on vire 3,5 et 9.

Il reste 0,4, et 8.

Or,

ne peut avoir pour unité seulement 0,6 ou 8.

Il ne reste donc que deux unités possibles : 0 et 8.

et

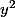
ont donc pour chiffre d'unité 1 ou 9 : 1 si

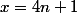
et 9 si

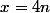
(on peut le savoir car la variation du chiffre des unité de

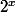
est périodique).

Ce sont des conditions nécessaires mais pas suffisantes et je ne vois pas comment continuer...

PS : Aviateurpilot, j'ai regardé Google-Images-"Agadir", rien qu'en voyant la troisième photo, ça ne m'incite pas a y aller... lol

par **aviateurpilot** » 27 Juil 2006, 15:52

nekros a écrit:Bah ça marche quand même !

ça ne marche jamias dans ce cas là

Couples d'entiers

couples d'entiers

Qui est en ligne