Ardu problème diophantien.
34 messages
- Page 1 sur 2 - 1, 2
Ardu problème diophantien.
Bonjour @ tous.
Quel est le plus grand entier qu'on ne peut pas écrire sous la forme 227a + 419b + 1009c, a,b,c entiers naturels ?
ça se résout manuellement sur à peine une 1/2 page A4 (calculette autorisée pour les petits calculs et vérifications).
Ce triplet a été choisi au hasard parmi les nombres premiers.
Bon amusement
Quel est le plus grand entier qu'on ne peut pas écrire sous la forme 227a + 419b + 1009c, a,b,c entiers naturels ?
ça se résout manuellement sur à peine une 1/2 page A4 (calculette autorisée pour les petits calculs et vérifications).
Ce triplet a été choisi au hasard parmi les nombres premiers.
Bon amusement
Re: Ardu problème diophantien.
Non, ce n'est pas 227*419-1 , Aviateur.
Même avec 227a + 419b seuls, c'est 227*419-227-419. Alors il est évident qu'avec 1009 en plus, on doit certainement trouver plus petit.
Je ne faisais pas d'humour quand je disais dans le titre que c'est difficile à trouver.
Même avec 227a + 419b seuls, c'est 227*419-227-419. Alors il est évident qu'avec 1009 en plus, on doit certainement trouver plus petit.
Je ne faisais pas d'humour quand je disais dans le titre que c'est difficile à trouver.
Re: Ardu problème diophantien.
j'imagine un programme info qui recherche le plus petit nombre 419b(k) + 1009c(k) tel que :
419b(k) + 1009c(k)=k modulo 227
et un majorant du nombre recherché est 419 max b(k) + 1009 max c(k)
419b(k) + 1009c(k)=k modulo 227
et un majorant du nombre recherché est 419 max b(k) + 1009 max c(k)
Re: Ardu problème diophantien.
nodgim a écrit:Non, ce n'est pas 227*419-1 , Aviateur.
Bonjour c'est exact j'ai dû me tromper (dans les calculs)mais je n'ai rien noté .
Je viens vite de recommencer avec seulement c=0 et effectivement je trouve un nbr + plus petit
:39001 (sauf erreur). Donc la réponse est au plus ce nombre
Re: Ardu problème diophantien.
Bonjour Nodgim et les autres 
Je n'ai pas cherché en détail ( on doit pouvoir trouver une formule générale pour trois entiers premiers quelconques ) . Une première piste pour deux entiers premiers p et q :
Les q entiers : 0 , p , 2p , 3p , ... , (q-1)p sont distincts modulo q donc ( toujours modulo q ) tous les entiers supérieurs ou égaux à 0 et congrus à 0 , supérieurs ou égaux à p et congrus à p , supérieurs ou égaux à 2p et congrus à 2p , ... , supérieurs ou égaux à (q-1)p et congrus à (q-1)p sont accessibles .
On peut ainsi trouver une borne supérieure pour le dernier entier inaccessible .
On peut procéder de même pour chacune des trois paires et peut-être réduire la hauteur de la borne .
Le travail n'est pas fini
Imod

Je n'ai pas cherché en détail ( on doit pouvoir trouver une formule générale pour trois entiers premiers quelconques ) . Une première piste pour deux entiers premiers p et q :
Les q entiers : 0 , p , 2p , 3p , ... , (q-1)p sont distincts modulo q donc ( toujours modulo q ) tous les entiers supérieurs ou égaux à 0 et congrus à 0 , supérieurs ou égaux à p et congrus à p , supérieurs ou égaux à 2p et congrus à 2p , ... , supérieurs ou égaux à (q-1)p et congrus à (q-1)p sont accessibles .
On peut ainsi trouver une borne supérieure pour le dernier entier inaccessible .
On peut procéder de même pour chacune des trois paires et peut-être réduire la hauteur de la borne .
Le travail n'est pas fini

Imod
Re: Ardu problème diophantien.
@ Aviateur: ce n'est pas 39001 (je renonce à chercher la combi qui donne ce nombre, la méthode que j'emploie pour trouver la solution ne passe pas par la connaissance de chaque nombre ! ). Sinon, je serais curieux de savoir qu'est ce qui t'a amené à trouver ce 39001.
@ Imod:
Salut à toi, ça fait un moment qu'on n'a pas correspondu. Ton problème posé ici sur les points et les droites est vraiment inaccessible, je n'ai pas insisté.
Sinon, il faut renoncer à trouver une formule générale comme avec 2 entiers. ça n'existe pas. Ce problème n'est vraiment pas facile, je ne suis arrivé à un truc abouti qu'après plusieurs améliorations successives.
@Pascal 16 et aux autres: un programme permettrait en effet de donner le résultat exact et de tester les valeurs trouvées à la main.
Sinon, vous pouvez essayer de trouver une solution avec un triplet plus petit pour commencer, du genre (7,11,19) par exemple.
@ Imod:
Salut à toi, ça fait un moment qu'on n'a pas correspondu. Ton problème posé ici sur les points et les droites est vraiment inaccessible, je n'ai pas insisté.
Sinon, il faut renoncer à trouver une formule générale comme avec 2 entiers. ça n'existe pas. Ce problème n'est vraiment pas facile, je ne suis arrivé à un truc abouti qu'après plusieurs améliorations successives.
@Pascal 16 et aux autres: un programme permettrait en effet de donner le résultat exact et de tester les valeurs trouvées à la main.
Sinon, vous pouvez essayer de trouver une solution avec un triplet plus petit pour commencer, du genre (7,11,19) par exemple.
Re: Ardu problème diophantien.
Rebonjour
J'ai trouvé 17918. Bref je suis assez sûr de ma méthode mais pas de tous les calculs, c'est vrai que c'est un peu fastidieux.
J'ai trouvé 17918. Bref je suis assez sûr de ma méthode mais pas de tous les calculs, c'est vrai que c'est un peu fastidieux.
Re: Ardu problème diophantien.
Rebonjour
Je n'ai pas dit que c'est 39001 mais au plus 39001. D'autre part je ne teste pas chaque nombre, d'ailleurs même avec un algo pas trop travaillé, je ne sais pas si on y arrive.
J'ai simplement raisonné par analyse synthèse, donc rien de bien compliqué. Vu mon erreur initiale j'ai repris mon premier travail en partie pour voir que la solution est au plus 39001. Ensuite j'ai repris la suite et je trouve la solution que j'ai donnée dans le post avant.
Néanmoins, j'ai un petit doute sur mon résultat précédent car il faudrait repasser en détails l'ensemble et je n'ai pas trop envie de le faire, tout au moins maintenant. (En particulier j'ai des inégalités strictes ou larges dont je n'ai pas trop fait attention).
17918 ça me semble correct non?
Je n'ai pas dit que c'est 39001 mais au plus 39001. D'autre part je ne teste pas chaque nombre, d'ailleurs même avec un algo pas trop travaillé, je ne sais pas si on y arrive.
J'ai simplement raisonné par analyse synthèse, donc rien de bien compliqué. Vu mon erreur initiale j'ai repris mon premier travail en partie pour voir que la solution est au plus 39001. Ensuite j'ai repris la suite et je trouve la solution que j'ai donnée dans le post avant.
Néanmoins, j'ai un petit doute sur mon résultat précédent car il faudrait repasser en détails l'ensemble et je n'ai pas trop envie de le faire, tout au moins maintenant. (En particulier j'ai des inégalités strictes ou larges dont je n'ai pas trop fait attention).
17918 ça me semble correct non?
Modifié en dernier par aviateur le 14 Juil 2018, 19:50, modifié 1 fois.
Re: Ardu problème diophantien.
Salut,
Et, toujours sauf erreur, à part le cas N=2 où il y a une jolie formule très simple à démontrer (si on s'y prend comme il faut...), dans le cas où N>=3, on n'a pas de formule explicite, mais uniquement des algorithmes plus ou moins efficaces.
Sauf erreur, ça s'appelle "le problème de Frobenius" dans la cas général avec N nombres.Imod a écrit:Je n'ai pas cherché en détail ( on doit pouvoir trouver une formule générale pour trois entiers premiers quelconques ) . Une première piste pour deux entiers premiers p et q :
Et, toujours sauf erreur, à part le cas N=2 où il y a une jolie formule très simple à démontrer (si on s'y prend comme il faut...), dans le cas où N>=3, on n'a pas de formule explicite, mais uniquement des algorithmes plus ou moins efficaces.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ardu problème diophantien.
@ Aviateur : 39001 = 150 * 227 + 7 * 419 + 2 * 1009
@ Ben314 : c'est tout à fait ça. Cependant, quand on a dit que ce sont les nombres de Frobenius, mis à part donner un peu de référence à la question, on n'a pas beaucoup avancé.
@ Ben314 : c'est tout à fait ça. Cependant, quand on a dit que ce sont les nombres de Frobenius, mis à part donner un peu de référence à la question, on n'a pas beaucoup avancé.
Re: Ardu problème diophantien.
@ Aviateur : 17918 est le bon nombre, bravo (je n'avais pas lu ton dernier message) !
Maintenant, si tu l'as fait en manuel, c'est super, mais il faut nous dire comment tu t'y es pris.
Maintenant, si tu l'as fait en manuel, c'est super, mais il faut nous dire comment tu t'y es pris.
Re: Ardu problème diophantien.
Bonjour
Je finis avec un petit algo malgré tout (voir si on peut sans passer)
Je sais que la solution est <= 39001 et je montre que si il existe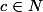 tel que
tel que
\geq \frac{1}{419} (-86 c+395 p)) alors p est une solution.
alors p est une solution.
remarque c prend approximativement au plus 38 valeurs.
Avec une machine je crée une fonction f(p) qui prend la valeur 1 s'il y a une solution 0 sinon.
Cela demande ( 2 lignes) et une petit boucle qui descend à partir de 39001 pour s'arrêter à 17918
plus grande valeur telle que f(p)=0. C'est très court en écriture et en temps 1mn sans faire d'effort. mais on peut accélérer mais à quoi cela servira-t-il?
Je finis avec un petit algo malgré tout (voir si on peut sans passer)
Je sais que la solution est <= 39001 et je montre que si il existe
remarque c prend approximativement au plus 38 valeurs.
Avec une machine je crée une fonction f(p) qui prend la valeur 1 s'il y a une solution 0 sinon.
Cela demande ( 2 lignes) et une petit boucle qui descend à partir de 39001 pour s'arrêter à 17918
plus grande valeur telle que f(p)=0. C'est très court en écriture et en temps 1mn sans faire d'effort. mais on peut accélérer mais à quoi cela servira-t-il?
Re: Ardu problème diophantien.
OK Aviateur. On ne peut pas vraiment dire que c'est une méthode manuelle, cela dit la construction de ton algo est astucieuse et efficace.
Bien entendu, " à quoi ça sert " élude la question : Du moment qu'on sait le faire avec l'informatique, à quoi ça sert de le faire à la main ? Pourquoi est ce qu'on s'embête encore à étudier des courbes quand une machine répond instantanément à ce qu'on veut savoir ?
Je donne ici un aperçu du mode d'emploi, tu vas voir que c'est très court à la main.
Après avoir trouvé que 1009 * -88 = 419 [227] (ce n'est pas bien long à trouver ça), on établit ce petit tableau:
419.............1009
1.....................-88
2.....................51
3....................-37
5.....................14
13...................-9
18....................5
qui se construit très rapidement.
Je m'intéresse aux 3 dernières lignes du tableau.
Après avoir vérifié (pas vraiment utile de le faire, mais ça rassure) que 18*9+13*14-13*9 = 227.
La solution est le max de (18-1)*419 + (9-1)*1009-227 ou (14-1) * 1009 + (13-1) * 419-227.
Soit 17918.
Et voilà.
Bien entendu, " à quoi ça sert " élude la question : Du moment qu'on sait le faire avec l'informatique, à quoi ça sert de le faire à la main ? Pourquoi est ce qu'on s'embête encore à étudier des courbes quand une machine répond instantanément à ce qu'on veut savoir ?
Je donne ici un aperçu du mode d'emploi, tu vas voir que c'est très court à la main.
Après avoir trouvé que 1009 * -88 = 419 [227] (ce n'est pas bien long à trouver ça), on établit ce petit tableau:
419.............1009
1.....................-88
2.....................51
3....................-37
5.....................14
13...................-9
18....................5
qui se construit très rapidement.
Je m'intéresse aux 3 dernières lignes du tableau.
Après avoir vérifié (pas vraiment utile de le faire, mais ça rassure) que 18*9+13*14-13*9 = 227.
La solution est le max de (18-1)*419 + (9-1)*1009-227 ou (14-1) * 1009 + (13-1) * 419-227.
Soit 17918.
Et voilà.
Re: Ardu problème diophantien.
Bonjour
C'est un problème que je ne connaissais pas mais je trouve la solution sans avoir fait une étude approfondie et dans cette situation il est logique d'avoir recours à la machine.
Je trouve que la remarque de @ben fait bien avancer les choses en faisant remarquer que c'est un problème connu.
Maintenant @Nogdim à part ton tableau de congruence modulo 227 je ne vois pas très bien le raisonnement.
Cela mérite quelques éclaircissement.
C'est un problème que je ne connaissais pas mais je trouve la solution sans avoir fait une étude approfondie et dans cette situation il est logique d'avoir recours à la machine.
Je trouve que la remarque de @ben fait bien avancer les choses en faisant remarquer que c'est un problème connu.
Maintenant @Nogdim à part ton tableau de congruence modulo 227 je ne vois pas très bien le raisonnement.
Cela mérite quelques éclaircissement.
Re: Ardu problème diophantien.
Oui, Aviateur, je me doute bien que je n'ai rien expliqué. Cependant, la justification est tellement longue que je ne la ferais que si on veut bien prendre la peine de la lire. A quoi ça me servirait d'écrire un truc que personne ne lira ?
Re: Ardu problème diophantien.
Bonjour @Nogdim
Il y a deux possibilités ou bien c'est toi qui a trouvé la démo ou alors tu l'as trouvé quelque part. Dans ce deuxième cas tu peux au moins donner la référence. Sinon une copie en image attaché c'est possible ou même les étapes de la démonstration cela suffit. Maintenant je ne pense pas que personne ne lira la démo, au contraire.
Il y a deux possibilités ou bien c'est toi qui a trouvé la démo ou alors tu l'as trouvé quelque part. Dans ce deuxième cas tu peux au moins donner la référence. Sinon une copie en image attaché c'est possible ou même les étapes de la démonstration cela suffit. Maintenant je ne pense pas que personne ne lira la démo, au contraire.
Re: Ardu problème diophantien.
La méthode est perso, et je crois bien qu'elle n'a jamais été établie jusqu'à maintenant. Les matheux étudient davantage les propriétés des relations plutôt que l'usage qu'on peut en faire. Elle est justifiée par une série de propriétés assez intéressantes dont la démo n'est jamais très compliquée.
Alors je vais plutôt proposer ici de justifier des propriétés, on arrivera ainsi à la méthode succinctement décrite plus naturellement.
1ère propriété
Soit (a<b<c) 3 entiers de N premiers entre eux 2 à 2. Soit un tableau de a*a cases avec en 1ère ligne les" a" multiples de c (de 0*c à (a-1)c ) et en 1ère colonne les "a" multiples de b (de 0*b à (a-1)b). Les autres cases du tableau sont remplies par la somme des têtes de ligne et colonne correspondantes. Soit enfin pour chaque case la valeur modulo "a" (la case comporte la valeur réelle R et la valeur mod " a " C)
Soit les "a" valeurs distinctes C trouvées dans le tableau, correspondant chacune à la plus petite valeur réelle R.
Prouver que l'ensemble de ces "a" valeurs forment un ensemble connexe dans le tableau.
J'espère que la question est claire.
Alors je vais plutôt proposer ici de justifier des propriétés, on arrivera ainsi à la méthode succinctement décrite plus naturellement.
1ère propriété
Soit (a<b<c) 3 entiers de N premiers entre eux 2 à 2. Soit un tableau de a*a cases avec en 1ère ligne les" a" multiples de c (de 0*c à (a-1)c ) et en 1ère colonne les "a" multiples de b (de 0*b à (a-1)b). Les autres cases du tableau sont remplies par la somme des têtes de ligne et colonne correspondantes. Soit enfin pour chaque case la valeur modulo "a" (la case comporte la valeur réelle R et la valeur mod " a " C)
Soit les "a" valeurs distinctes C trouvées dans le tableau, correspondant chacune à la plus petite valeur réelle R.
Prouver que l'ensemble de ces "a" valeurs forment un ensemble connexe dans le tableau.
J'espère que la question est claire.
Re: Ardu problème diophantien.
Bonjour @nogdim. Passons pour l'instant les démonstration et regardons ta méthode.
Voici ton tableau avec le petit exemple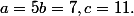
 & \left(\begin{array}{c}<br /> 11 \\ 1\end{array}\right) & \left(\begin{array}{c} 22 \\ 2\end{array}\right) & \left(\begin{array}{c} 33 \\ 3\end{array}\right) & \left(\begin{array}{c} 44 \\ 4\end{array}\right) \\ \left(\begin{array}{c} 7 \\ 2<br />\end{array}\right) & \left(\begin{array}{c} 18 \\ 3\end{array}\right) & \left(\begin{array}{c} 29 \\ 4\end{array}<br />\right) & \left(\begin{array}{c} 40 \\ 0\end{array}\right) & \left(\begin{array}{c} 51 \\ 1\end{array}\right) \\ \left(<br />\begin{array}{c} 14 \\ 4\end{array}\right) & \left(\begin{array}{c} 25 \\ 0\end{array}\right) & \left(\begin{array}{c} 36 \\ 1\end{array}\right) & \left(\begin{array}{c} 47 \\ 2\end{array}\right) & \left(\begin{array}{c} 58 \\ 3\end{array}\right) \\ \left(\begin{array}{c} 21 \\ 1\end{array}\right) & \left(\begin{array}{c} 32 \\ 2\end{array}\right) & \left(\begin{array}{c} 43 \\ 3\end{array}\right) & \left(\begin{array}{c} 54 \\ 4\end{array}\right) & \left(\begin{array}{c} 65 \\ 0\end{array}\right) \\ \left(\begin{array}{c} 28 \\ 3\end{array}\right) & \left(\begin{array}{c} 39 \\ 4\end{array}\right) & \left(\begin{array}{c} 50 \\ 0\end{array}\right) & \left(\begin{array}{c} 61 \\ 1\end{array}\right) & \left(\begin{array}{c} 72 \\ 2\end{array}\right)\end{array}\right))
Qu'est ce qui est connexe?
Voici ton tableau avec le petit exemple
Qu'est ce qui est connexe?
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
