Simplification d'une fraction de racine carrée
Réponses à toutes vos questions du CP à la 3ème
-
jean fi
- Messages: 6
- Enregistré le: 24 Déc 2015, 19:31
-
 par jean fi » 24 Déc 2015, 19:38
par jean fi » 24 Déc 2015, 19:38
Bonjour, pourriez vous m'aider à simplifier la fraction de racine carrée suivante:
V(1+v(1+((1+v5)/2)))
merci de votre aide et bonnes fêtes de noël
-
mathelot
 par mathelot » 24 Déc 2015, 19:49
par mathelot » 24 Déc 2015, 19:49
jean fi a écrit:Bonjour, pourriez vous m'aider à simplifier la fraction de racine carrée suivante:
V(1+v(1+((1+v5)/2)))
merci de votre aide et bonnes fêtes de noël
Pose

démontre en élevant au carré l'égalité
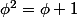 (1)
(1)
grâce à l'égalité
(1), les racines vont se simplifier
-
jean fi
- Messages: 6
- Enregistré le: 24 Déc 2015, 19:31
-
 par jean fi » 25 Déc 2015, 13:06
par jean fi » 25 Déc 2015, 13:06
mathelot a écrit:Pose

démontre en élevant au carré l'égalité
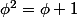 (1)
(1)
grâce à l'égalité
(1), les racines vont se simplifier
BONJOUR MATHELOT
JE VOUS REMERCIE POUR VOTRE AIDE RAPIDE ET VOUS SOUHAITE UN JOYEUX NOEL
J'ai démontré cette égalité cependant je ne trouve pas le bon résultat de cette équation et comment je peux développer en posant fi pour simplifier l'équation
pourriez vous m'aider une nouvel fois
merci Mathelot

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 25 Déc 2015, 13:40
par laetidom » 25 Déc 2015, 13:40
jean fi a écrit:BONJOUR MATHELOT
JE VOUS REMERCIE POUR VOTRE AIDE RAPIDE ET VOUS SOUHAITE UN JOYEUX NOEL
J'ai démontré cette égalité cependant je ne trouve pas le bon résultat de cette équation et comment je peux développer en posant fi pour simplifier l'équation
pourriez vous m'aider une nouvel fois
merci Mathelot
Bonjour à tous et joyeux Noël !,
en fin de compte, en suivant ce que t'a dit mathelot, tu obtiens que
 et cette fraction s'appelle le nombre d'or !
et cette fraction s'appelle le nombre d'or !en effet, déjà 1ère vérification avec la calculatrice,

1.618033989....
et

1.618033989....
en prenant la suite de mathelot, si

alors

donc




Bonne journée de Noël.
.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 25 Déc 2015, 23:20
par Pisigma » 25 Déc 2015, 23:20
jean fi a écrit:Bonjour, pourriez vous m'aider à simplifier la fraction de racine carrée suivante:
V(1+v(1+((1+v5)/2)))
merci de votre aide et bonnes fêtes de noël
Bonsoir,
Une autre façon de développer:

^2}{4}}=\dfrac{1+sqrt{5}}{2})

Un peu tard mais bonne fête de Noël :lol3:
-
mathelot
 par mathelot » 25 Déc 2015, 23:25
par mathelot » 25 Déc 2015, 23:25
Du point de vue pédagogique, il vaut mieux poser

,
ce qui prépare aux calculs en nombres complexes.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 25 Déc 2015, 23:32
par Pisigma » 25 Déc 2015, 23:32
mathelot a écrit:Du point de vue pédagogique, il vaut mieux poser

,
ce qui prépare aux calculs en nombres complexes.
Je suis tout à fait d'accord avec toi.C'était certainement le but, un peu caché, de l'exercice.
Toutefois, il est parfois bon de pouvoir simplifier les radicaux.
-
jean fi
- Messages: 6
- Enregistré le: 24 Déc 2015, 19:31
-
 par jean fi » 26 Déc 2015, 11:10
par jean fi » 26 Déc 2015, 11:10
laetidom a écrit:Bonjour à tous et joyeux Noël !,
en fin de compte, en suivant ce que t'a dit mathelot, tu obtiens que
 et cette fraction s'appelle le nombre d'or !
et cette fraction s'appelle le nombre d'or !en effet, déjà 1ère vérification avec la calculatrice,

1.618033989....
et

1.618033989....
en prenant la suite de mathelot, si

alors

donc




Bonne journée de Noël.
.
bonjour à vous,
merci beaucoup pour votre aide, effectivement cela appel à appréhender les nombres complexes dans un second temps
un grand merci

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 26 Déc 2015, 11:13
par laetidom » 26 Déc 2015, 11:13
jean fi a écrit:bonjour à vous,
merci beaucoup pour votre aide, effectivement cela appel à appréhender les nombres complexes dans un second temps
un grand merci
Bonjour,
Contents d'avoir pu être utiles ! @+ sur le forum.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Déc 2015, 19:17
par Ben314 » 26 Déc 2015, 19:17
mathelot a écrit:Du point de vue pédagogique, il vaut mieux poser

,
ce qui prépare aux calculs en nombres complexes.
C'est quoi le rapport entre le nombre d'Or et les nombres complexes ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 26 Déc 2015, 19:28
par mathelot » 26 Déc 2015, 19:28
Ben314 a écrit:C'est quoi le rapport entre le nombre d'Or et les nombres complexes ?
chaque fois qu'on a
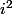
dans un calcul , on le remplace par -1 et chaque fois qu'on a
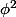
, on le remplace par
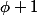
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
(1)
et cette fraction s'appelle le nombre d'or !
1.618033989....
1.618033989....
alors



