Résoudre équitation premier degré

[tricova]

Bonjour, je suis actuellement un cour qui présente la résolution d'équation comme suit :

chercher la valeur de x pour laquelle l'égalité pour laquelle 2x-7 = 0 est vraie

2x-7=0
si deux nombres sont égaux et qu'on ajoute à chacun le même nombre alors ils sont toujours égaux
ajoutons 7 à chaque membres de l'égalité :
2x-7+7 =0 + 7
on obtient 2x=7
si deux nombres sont égaux et qu'on divise chacun d'eux par un même nombre non nul alors ils restent également égaux
divisons par exemple chaque membres de l'égalité par deux
2x/2 = 7/2
on obtient alors la solution x=7/2



ce que je ne comprends pas c'est pourquoi seulement x=7/2 ? alors que ça devrait être selon moi 2x=7/2 ?

svp
merci d'avance

[Pisigma]

Bonjour,

[focon]

parce que 2x/2 = x

[WillyCagnes]

bjr

tu obtiens 2x=7
il suffit de diviser par 2 les 2 membres de l'equation
x=7/2 tout simplement

essaie de résoudre
9x +10=0

[laetidom]

Bonjour @ tous,

tricova, petite aide supplémentaire . . .

7divisé par 2.JPG (24.07 Kio) Vu 1201 fois

et petite vérification : 2x=7 avec x=7/2 donne 2.(7/2) = 7 ===> c'est juste

et avec ton 2x=7/2 donc x=7/4 que l'on remet dans l'équation de départ 2x-7=0 ===> ça donnerait 7/2 - 7 = 0 ce qui est faux ! . . .

[tricova]

Bonjour, merci pour vos réponses

J'étais parti du principe qu'il fallait d'abord multiplier 2 fois x et ensuite diviser, mais apparemment dans la mesure ou on ne connait pas x il n'y a pas de multiplication.

essaie de résoudre
9x +10=0

9x+10-10=0-10
9x=-10
9x/9=-10:9
x=1.11111

[laetidom]

Salut,

Solution de l'équation 9x+10=0 donne S = { -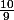 } suffit, inutile de rajouter 1.111111 qui est en fait - 1.11111 mais qui n'est pas finie ....donc l'écriture fractionnaire est celle attendue !


vérif : 9x+10=0
avec x=-10/9 donne 9.(-10/9)+10 donne -10+10 qui est bien égal à 0 donc l'équation est vérifiée !

[mouette 22]

IL faut bien rire un peu même en début d'année scolaire !

Mais qui a donc écrit :

RESOUDRE "EQUITATION"PREMIER DEGRE ???? Quelqu 'un qui fait du cheval ?

[Lostounet]

IL faut bien rire un peu même en début d'année scolaire !

Mais qui a donc écrit :

RESOUDRE "EQUITATION"PREMIER DEGRE ???? Quelqu 'un qui fait du cheval ?

Hahahahahahahah

[laetidom]

Oui effectivement ! (sourire), je n'avais pas remarqué ce lapsus, peut-être révélateur . . . ? . . .