[Défi**] Racines carrées (3e-2nde)
Réponses à toutes vos questions du CP à la 3ème
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Déc 2009, 02:51
par Dinozzo13 » 28 Déc 2009, 02:51
Bonjour, aujourd'hui je propose un défi de mon invention, surtout destiné pour les 3e, voire 2nde s'il y en a ici, afin d'appronfondir votre réflexion sur les calculs avec des racines carrées, bon travail :++:
La difficulté semble être croissante tout au long de l'exercice ^^Calculer, lorsque cela est possible, les nombres suivants :
1°)
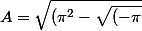^2})^2})
2°)
^2}+\sqrt{(\sqrt2 -\pi)^2}\right)^2})
3°)
^2\right)^2\right)^2+\left(\sqrt{\left(-\sqrt{(\sqrt7+7)^2\right)^2\right)^2)
4°)
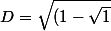^2}+\sqrt{(\sqrt1-1)^2}+\sqrt{(2-\sqrt2)^2}+\sqrt{(\sqrt2-2)^2}+\sqrt{(3-\sqrt3)^2}+\sqrt{(\sqrt3-3)^2}+...+\sqrt{(1000-\sqrt{1000})^2}+\sqrt{(\sqrt{1000}-1000)^2})
Inutile de vous dire qu'il faut réfléchir et non pas foncer comme un bourin :ptdr:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Déc 2009, 14:37
par Dinozzo13 » 28 Déc 2009, 14:37
:hum: ce n'est pas très glorieux tout ça. Un petit indice ?
-
lysli
- Membre Rationnel
- Messages: 875
- Enregistré le: 16 Fév 2006, 00:07
-
 par lysli » 28 Déc 2009, 14:52
par lysli » 28 Déc 2009, 14:52
c'est pas dur c'est jute long et chiant à calculer :marteau:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2009, 05:07
par Dinozzo13 » 29 Déc 2009, 05:07
Ce n'est pas complètement vrai, car sinon je l'aurais mis au lycée. Mais si cela était trop simple et visiblement trop rapide, cette discussion n'aurait pas lieu d'être. :hum:
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 29 Déc 2009, 10:13
par oscar » 29 Déc 2009, 10:13
Cmme personne ne se décife
A = V ( p² -pi²=
C) V [- ( v7-7)] ² + V [ -( v7+7)]²=
-
lysli
- Membre Rationnel
- Messages: 875
- Enregistré le: 16 Fév 2006, 00:07
-
 par lysli » 29 Déc 2009, 11:21
par lysli » 29 Déc 2009, 11:21
Dinozzo13 a écrit: Ce n'est pas complètement vrai, car sinon je l'aurais mis au lycée. Mais si cela était trop simple et visiblement trop rapide, cette discussion n'aurait pas lieu d'être.
Ben quand on connaît son cours, faut juste l'appliquer en faisant attention aux signes, c'est l'histoire des carrés tout ca ...
Exemple :
2°)
^2}+\sqrt{(\sqrt2 -\pi)^2}\right)^2}\\<br />B=2\left(\sqrt{\left(\sqrt{(\pi-\sqrt2)^2}+\sqrt{(\sqrt2 -\pi)^2}\right)}\right)^2\\<br />B=2(\sqrt{(\pi-\sqrt2)^2}+\sqrt{(\sqrt2 -\pi)^2})\\<br />...)
C'est pas très difficile :doh:
-
Anonyme
 par Anonyme » 20 Fév 2010, 16:59
par Anonyme » 20 Fév 2010, 16:59
Sauf que c'est faux...

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 20 Fév 2010, 20:34
par Lostounet » 20 Fév 2010, 20:34
Dinozzo13 a écrit:Bonjour, aujourd'hui je propose un défi de mon invention, surtout destiné pour les 3e, voire 2nde s'il y en a ici, afin d'appronfondir votre réflexion sur les calculs avec des racines carrées, bon travail :++:
La difficulté semble être croissante tout au long de l'exercice ^^Calculer, lorsque cela est possible, les nombres suivants :
1°)
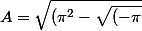^2})^2})
2°)
^2}+\sqrt{(\sqrt2 -\pi)^2}\right)^2})
3°)
^2\right)^2\right)^2+\left(\sqrt{\left(-\sqrt{(\sqrt7+7)^2\right)^2\right)^2)
4°)
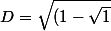^2}+\sqrt{(\sqrt1-1)^2}+\sqrt{(2-\sqrt2)^2}+\sqrt{(\sqrt2-2)^2}+\sqrt{(3-\sqrt3)^2}+\sqrt{(\sqrt3-3)^2}+...+\sqrt{(1000-\sqrt{1000})^2}+\sqrt{(\sqrt{1000}-1000)^2})
Inutile de vous dire qu'il faut réfléchir et non pas foncer comme un bourin :ptdr:
1)
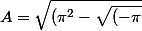^2})^2}<br /><br />= \sqrt{\pi^2 - {\pi}}^2)
On sait effectivement que

.
Il est possible d'annuler le radical !
Ensuite, on factorise l'expression obtenue ?!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 20 Fév 2010, 21:45
par Lostounet » 20 Fév 2010, 21:45
En fait, j'ai essayé de toutes les faires, et ça a marché je pense, sans problème (la calculatrice confirme aussi).
Pour la dernière, on pourrait appliquer la technique du n(n+1) divisé par 2 hein?
La C est très méchante !!
Au fait, j'adore tes défis Dinozzo :id:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités