Mon fils a un petit exercice de maths pour démarrer l'année sur lequel il séche lamentablement... Moi aussi !
Le voici :
Parmi tous les nombres inférieurs à 1000, combien ont pour somme des chiffres la valeur 9 (ex : 333, 54, 18, 540...)
Bien entendu on peut dénombrer, mais comment arriver à la réponse mathématiquement parlant. J'ai tenté une mise en équation, des calculs de proba... mais les maths sont loin pour moi !!
Merci de votre aide
Kalisand
Nombres dont la somme des chiffres est...
8 messages
- Page 1 sur 1
Kalisand a écrit:Mon fils a un petit exercice de maths pour démarrer l'année sur lequel il séche lamentablement... Moi aussi !
Le voici :
Parmi tous les nombres inférieurs à 1000, combien ont pour somme des chiffres la valeur 9 (ex : 333, 54, 18, 540...)
Bien entendu on peut dénombrer, mais comment arriver à la réponse mathématiquement parlant. J'ai tenté une mise en équation, des calculs de proba... mais les maths sont loin pour moi !!
Merci de votre aide
Kalisand
Si l'on choisit les deux premiers chiffres, le troisième est automatiquement déterminé. Donc le choix se fait seulement sur les deux derniers chiffres.
Si la somme des deux premiers chiffres est 9, il y a dix possibilités :
09,18,27,36,45,54,63,72,81,90 : pour chaque cas il faut mettre 0 en troisième chiffre
Si la somme des deux premiers chiffres est 8, il y a neuf possibilités :
08,17,26,35,44,53,62,71,80 : pour chaque cas il faut mettre 1 en troisième chiffre
etc...
Si la somme des deux premiers chiffres est 0, il y a une possibilité :
00: pour chaque cas il faut mettre 9 en troisième chiffre
Donc, en tout, il y a 1+2+...+9+10 soit 55 possibilités.
On peut dire que les nombres qui ont cette propriété sont divisibles par 9. Or pour être divisible par 9 un nombre doit avoir la somme de ses chiffres multiple de 9 : soit 0, 9, 18 ou 27. Pour 0 il n'y a que 000. Pour 27 il n'y a que 999. En calculant le nombre de nombres dont la somme des chiffres est 18, on aura tous les multiples de 9 entre 0 et 999, c'est à dire 0*9, 1*9,...111*9 soit 112 nombres.
Pour trouver les nombres dont la somme des chiffres est 18, il suffit pour chaque nombre listé ci-dessus, de remplacer chaque chiffre par le complément à 9 : par exemple 009 (somme 9) donne 990 (somme 18)
126 (somme 9) donne 873 (somme (18)
Par conséquent le nombre des nombres dont la somme des chiffres est 18 est exactement égal à celui des nombres dont la somme des chiffres est 9, soit 55.
On vérifie effectivement que le nombre des multiples de 9 (112) est bien égal au nombre des nombres dont la somme des chiffres est 0 (1) additionné au nombre des nombres dont la somme des chiffres est 9 (55) additionné au nombre des nombres dont la somme des chiffres est 18 (55) additionné au nombre des nombres dont la somme des chiffres est 27 (1) :
112 = 1 + 55 + 55 + 1
Ce n'était pas demandé, mais cela permet de vérifier notre calcul...
Bonjour,
Pour les fanas du dénombrement, remarquons qu'il s'agit d'un cas particulier du problème évoqué dans ce fil :
http://maths-forum.com/showthread.php?t=4765&page=1&pp=10
Le nombre de possibilités est bien :
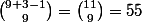
Nicolas
Pour les fanas du dénombrement, remarquons qu'il s'agit d'un cas particulier du problème évoqué dans ce fil :
http://maths-forum.com/showthread.php?t=4765&page=1&pp=10
Le nombre de possibilités est bien :
Nicolas
Nicolas_75 a écrit:Bonjour,
Pour les fanas du dénombrement, remarquons qu'il s'agit d'un cas particulier du problème évoqué dans ce fil :
http://maths-forum.com/showthread.php?t=4765&page=1&pp=10
Le nombre de possibilités est bien :
Nicolas
Très juste, mais puisque Kalisand "ne s'attendait pas à ce que l'explication fût si longue ! ", j'ai pensé qu'il fallait rester sur le cas particulier, plus accessible.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
