bonjour ,
je suis en 3eme
pourriez-vous m'aider à comprendre mon énoncé svp
je vous en remercie d'avance
voici un casier ou l'on ecrit un chiffre dans chacune des 10 cases
elles sont toutes sur la meme ligne
dans la 1ere,est écrit le nombre de fois ou apparait le chiffre 1 dans le casier
dans la 2eme, est écrit le nombre de fois ou apparait le chiffre 2 dans le casier
dans la 3ème, est écrit le nombre de fois ou apparait le chiffre 3 dans le casier
...
dans la 10ème, est écrit le nombre de fois ou apparait le chiffre 0 dans le casier
Enoncé de casier
10 messages
- Page 1 sur 1
Re: enoncé de casier
comprendre ou le resoudre ?
comprendre ben il faut mettre un chiffre dans le casier 3 par exemple tu mets 2,
ben alors cela veut dire que maintenant tu dois mettre deux fois le 3 dans d'autres casiers,
si tu mets 3 dans le 1 il faudra encore mettre trois fois le 1 dans d'autres casiers
et l'autre trois si tu le mets en position7, faudra mettre du 7 dans 3 casiers
comprendre ben il faut mettre un chiffre dans le casier 3 par exemple tu mets 2,
ben alors cela veut dire que maintenant tu dois mettre deux fois le 3 dans d'autres casiers,
si tu mets 3 dans le 1 il faudra encore mettre trois fois le 1 dans d'autres casiers
et l'autre trois si tu le mets en position7, faudra mettre du 7 dans 3 casiers
Modifié en dernier par beagle le 15 Sep 2018, 13:39, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: enoncé de casier
Tu vois donc ainsi assez rapidement que moins tu en fais mieux c'est, parce que faut vraiment pas trop remplir.
Que des zeros partout, pas mal mais à la fin faut mettre 10 dans le casier 10, 10 n'est pas un chiffre
mettre du 1 et des zeros ,
certainement beaucoup de zeros
si beaucoup de zeros par exemple 5 , ou 6 ou 7,
alors faudra mettre 5 ou 6 ou 7 dans le casier 10
et alors faudra bien mettre du 1 dans le casier 5 ou 6 ou 7 pour avoir celui du casier 10
Mais si tu mets du 1 au casier 5 ou 6 ou 7
faudra mettre 1 dans le casier 1,
ben du coup des 1 va y en avoir deux
oh ptain
donc,
je mets 2 dans le casier 1, et donc 1 dans le casier 2
et le reste en zero sauf le nombre de zeros
10 cases moins la 1 à 2, la 2 à 1 et la 10 qui aura le nombre de zero, moins la case nombre de zero
c'est 10-4, je mets le 1 nombre de zero en case 6
on essaye donc:
2100010006
Que des zeros partout, pas mal mais à la fin faut mettre 10 dans le casier 10, 10 n'est pas un chiffre
mettre du 1 et des zeros ,
certainement beaucoup de zeros
si beaucoup de zeros par exemple 5 , ou 6 ou 7,
alors faudra mettre 5 ou 6 ou 7 dans le casier 10
et alors faudra bien mettre du 1 dans le casier 5 ou 6 ou 7 pour avoir celui du casier 10
Mais si tu mets du 1 au casier 5 ou 6 ou 7
faudra mettre 1 dans le casier 1,
ben du coup des 1 va y en avoir deux
oh ptain
donc,
je mets 2 dans le casier 1, et donc 1 dans le casier 2
et le reste en zero sauf le nombre de zeros
10 cases moins la 1 à 2, la 2 à 1 et la 10 qui aura le nombre de zero, moins la case nombre de zero
c'est 10-4, je mets le 1 nombre de zero en case 6
on essaye donc:
2100010006
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: enoncé de casier
Salut,
A mon avis, à la fin faudra forcément y aller à coup de test, mais au départ, il vaut mieux commencer par réfléchir de façon un peu globale pour voir ce qu'on peut dire des chiffres qui apparaissent dans les cases.
Par exemple, la somme des chiffres de toutes les cases, c'est pas compliqué de voir combien ça fait et en réfléchissant un peu plus, on peut même trouver combien vaut la somme des produit
Chiffre de la case Numero de la case
Numero de la case
(où les "numéros de cases" sont bien sûr 1,2,3,...,8,9,0)
Ensuite, cela laisse très peu de possibilités à étudier.
A mon avis, à la fin faudra forcément y aller à coup de test, mais au départ, il vaut mieux commencer par réfléchir de façon un peu globale pour voir ce qu'on peut dire des chiffres qui apparaissent dans les cases.
Par exemple, la somme des chiffres de toutes les cases, c'est pas compliqué de voir combien ça fait et en réfléchissant un peu plus, on peut même trouver combien vaut la somme des produit
Chiffre de la case
(où les "numéros de cases" sont bien sûr 1,2,3,...,8,9,0)
Ensuite, cela laisse très peu de possibilités à étudier.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: enoncé de casier
beagle a écrit:on essaye donc:
2100010006
salut beagle
Un test montre que c'est bien la seule solution
Re: enoncé de casier
Salut chan79, trop rare sur le forum!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: enoncé de casier
Mince, je croyais que Ben avait posé une question sur la généralisation. j'ai rêvé ?
Alors je réponds pour n cases, de 0 à n-1. Au passage, il me parait plus normal de placer la case 0 en tête.
Comme disait Ben, il n'y a pas 36 solutions :
1) La somme des nombres inscrits est égal au nombre de cases.
2) On ne peut pas mettre 0 dans la case 0.
3) La case 1 est auto référente c(1) = 1 se suffit. Ce qui implique qu'un 1 hors case 1 implique c(1)>1.
Donc on peut regarder ce qu'il se passe selon le nombre affiché dans la case 0.
c(0) = 1 : 1210. tentative 13110 : manque le 2. En le plaçant, il nous manquera les 2 numéros de cases affectées de 2. Ces 2 numéros appelleront au moins 2 autres numéros, qui eux mêmes appelleront....etc.
D'où l'impossibilité d'affecter un nombre > 2 dans la case 1.
c(0)= 2 : 2020 ou 21200.
c(0)=3 : 3211000.
c(0)=4: 42101000.
c(0)=n : n2100...1dans c(n)...0000.
Alors je réponds pour n cases, de 0 à n-1. Au passage, il me parait plus normal de placer la case 0 en tête.
Comme disait Ben, il n'y a pas 36 solutions :
1) La somme des nombres inscrits est égal au nombre de cases.
2) On ne peut pas mettre 0 dans la case 0.
3) La case 1 est auto référente c(1) = 1 se suffit. Ce qui implique qu'un 1 hors case 1 implique c(1)>1.
Donc on peut regarder ce qu'il se passe selon le nombre affiché dans la case 0.
c(0) = 1 : 1210. tentative 13110 : manque le 2. En le plaçant, il nous manquera les 2 numéros de cases affectées de 2. Ces 2 numéros appelleront au moins 2 autres numéros, qui eux mêmes appelleront....etc.
D'où l'impossibilité d'affecter un nombre > 2 dans la case 1.
c(0)= 2 : 2020 ou 21200.
c(0)=3 : 3211000.
c(0)=4: 42101000.
c(0)=n : n2100...1dans c(n)...0000.
Re: enoncé de casier
Non, tu avais pas rêve : j'avais effectivement mis une question, mais je l'ai enlevé en constatant après coup que c'était pas super intéressant. Je peut te mettre la suite des raisonnement que j'ai tenu (et pourquoi j'ai enlevé la question au final).
Le contexte, c'est évidement une suite d'entiers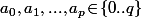 et, pour tout
et, pour tout 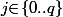 , l'entier
, l'entier ) (l'énoncé original, c'est donc
(l'énoncé original, c'est donc  et
et 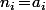 pour tout
pour tout  )
)
Évidement, on a=p\!+\!1)
Ensuite, en regroupant les tels que
tels que 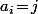 , on a aussi
, on a aussi 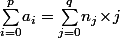
Ca signifie que, dans l'énoncé original on a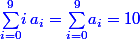 .
.
Là, ça sent plus que très fort que ces deux relations en bleu sont les deux premières d'une "suite logique" (à elles deux, elles ne sont évidement insuffisante pour traduire que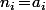 pour tout
pour tout  ).
).
Et je me demandais ce que pourrait être la "suite logique" de ces deux relations.
Et là, le truc qui a fini par me venir à l'esprit, c'est que le lien entre les et les
et les 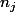 on pouvait l'écrire en terme de polynômes (formels)
on pouvait l'écrire en terme de polynômes (formels) 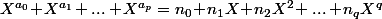 puis que :
puis que :
- L'égalité des deux polynômes en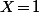 donnait la relation
donnait la relation 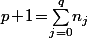
- L'égalité des dérivées des deux polynômes en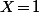 donnait la relation
donnait la relation 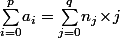
Et donc que la "logique", ben ça consistait à continuer à dériver et à regarder en X=1.
Par exemple la relation suivante serait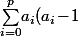=\sum_{j=0}^q \!n_j\!\times\!j(j\!-\!1))
Et qu'en écrivant ces relation jusqu'à atteindre le degré des deux polynôme, ça donnerais une C.N.S pour qu'ils soient égaux.
Et c'était ça mon "casse tête" : montrer l'équivalence entre l'énoncé original et les relations obtenues en prenant X=1 sur les relation en question.
Sauf que je me suis rendu compte que les relations en question, ben c'était complètement con vu que ce qu'elle disait, c'était des trucs du style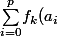=\sum_{j=0}^q \!n_j f_k(j)) qui se déduisent trivialement de la définition des
qui se déduisent trivialement de la définition des 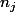 et que pour montrer que c'est des C.N.S. (pour que les
et que pour montrer que c'est des C.N.S. (pour que les 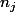 soient bien ce qu'ils son), ben y'avait juste à montrer que le système linéaire en les
soient bien ce qu'ils son), ben y'avait juste à montrer que le système linéaire en les 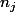 admettait une unique solution, c'est à dire que la matrice des
admettait une unique solution, c'est à dire que la matrice des \big)) était inversible [ce qui est assez trivial].
était inversible [ce qui est assez trivial].
Donc... j'ai enlevé le post...
Le contexte, c'est évidement une suite d'entiers
Évidement, on a
Ensuite, en regroupant les
Ca signifie que, dans l'énoncé original on a
Là, ça sent plus que très fort que ces deux relations en bleu sont les deux premières d'une "suite logique" (à elles deux, elles ne sont évidement insuffisante pour traduire que
Et je me demandais ce que pourrait être la "suite logique" de ces deux relations.
Et là, le truc qui a fini par me venir à l'esprit, c'est que le lien entre les
- L'égalité des deux polynômes en
- L'égalité des dérivées des deux polynômes en
Et donc que la "logique", ben ça consistait à continuer à dériver et à regarder en X=1.
Par exemple la relation suivante serait
Et qu'en écrivant ces relation jusqu'à atteindre le degré des deux polynôme, ça donnerais une C.N.S pour qu'ils soient égaux.
Et c'était ça mon "casse tête" : montrer l'équivalence entre l'énoncé original et les relations obtenues en prenant X=1 sur les relation en question.
Sauf que je me suis rendu compte que les relations en question, ben c'était complètement con vu que ce qu'elle disait, c'était des trucs du style
Donc... j'ai enlevé le post...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: enoncé de casier
merci à nodgim d'avoir relancé car j'avais aperçu le message de Ben314 hier soir.
Cela reste absolument passionnant de voir l'approche de ben314 sur un tel problème,
même si cela n'aboutit pas comme il le veut,
néanmoins trop compliqué pour moi.
Mais passionnant!
Cela reste absolument passionnant de voir l'approche de ben314 sur un tel problème,
même si cela n'aboutit pas comme il le veut,
néanmoins trop compliqué pour moi.
Mais passionnant!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
