Sur la racine carrée de i.
35 messages
- Page 1 sur 2 - 1, 2
Sur la racine carrée de i.
Avertissement. Partout les expressions en exposant n'ont pas été en exposant.
De plus, le symbole "radical" de la racine carrée a été remplacé par un A surligné.
Pourtant ,les indices et les exposants et le signe radical sont pris en compte sous word.
Par exemple, partout l'exposant 1/2 n'a pas été placé en exposant ce qui rend la lecture compliquée !
Ainsi, 11/2 doit être lu 1 puissance 1/2 et ça change tout !
Bonjour,
Il est fréquent, dans les ouvrages de vulgarisation, de lire la remarque suivante à propose de i, unité imaginaire :
« Il est faux d’écrire i = √(-1) » C’est vrai, mais ce jugement péremptoire pourrait faire croire que i n’est pas la racine carrée de -1 !
Eh bien, je vais démontrer formellement que i est bel et bien la racine carrée de -1 et que les vulgarisateurs appliquent bêtement un symbole qui n’a de sens que dans le corps des réels !
L’objection des vulgarisateurs se présente ainsi : i² = √(-1)√(-1)= √((-1)(-1) = 1 d’où la prétendue contradiction.
Pourtant, des auteurs d’une grande réputation (Richard Feynman et Roger Penrose par exemple), n’hésitent pas à écrire i =√(-1) ! Mais dans ce cas, et bien qu’effectivement une telle expression est formellement incorrecte, ils veulent simplement et par raccourci, écrire que la racine carrée de -1 est égale à i dans le corps des complexes.
Précisons bien que la racine carrée de 4 est ±2 alors que √(4) = 2 par définition du symbole √ dont le résultat se limite toujours à la racine positive.
Or, le concept de nombre positif et négatif n’existe pas dans le corps des nombres complexes !. Par conséquent, le symbole √, qui ne donne que la racine positive, n’a aucun sens dans le corps des complexes.
Mais tout rentre dans l’ordre si on écrit i = -11/2 et on a bien
i² =-11/2 -11/2 = -11/2+1/2 = -1
Et c’est parfaitement cohérent ! (rappel : La racine carrée d’un nombre n, réel ou complexe, peut s’écrire : n½, n étant strictement positif dans le cas des réels)
En effet, écrivons –11/2 = e1/2log(-1) (car ab =eblog(a) e est la base des logarithmes népériens (*))
Or, log(-1) = iπ (**)
d’où –11/2 = e1/2log(-1) = eiπ/2
Mais eiπ/2 = cos(π /2) + isin(π/2) = 0 + 1 car cos(π /2) = 0 et sin(π/2) =1
D’où finalement : –11/2 = i et i est bel et bien la racine carrée de -1 !
(*) e = 2.718…..)
(**) Rappel de la formule d’Euler : eiπ = -1 d’où log(-1) =iπ pour la même raison que, dans les logarithmes décimaux, donc à base 10, on a, par exemple :
103 = 1000, alors log(1000) = 3.
Moralité : Méfiez-vous comme de la peste des mauvais vulgarisateurs. Surtout de ceux qui prétendent vulgariser une science invulgarisable : La mécanique quantique sans mathématiques.
Merci de votre attention.
Cordialment.
De plus, le symbole "radical" de la racine carrée a été remplacé par un A surligné.
Pourtant ,les indices et les exposants et le signe radical sont pris en compte sous word.
Par exemple, partout l'exposant 1/2 n'a pas été placé en exposant ce qui rend la lecture compliquée !
Ainsi, 11/2 doit être lu 1 puissance 1/2 et ça change tout !
Bonjour,
Il est fréquent, dans les ouvrages de vulgarisation, de lire la remarque suivante à propose de i, unité imaginaire :
« Il est faux d’écrire i = √(-1) » C’est vrai, mais ce jugement péremptoire pourrait faire croire que i n’est pas la racine carrée de -1 !
Eh bien, je vais démontrer formellement que i est bel et bien la racine carrée de -1 et que les vulgarisateurs appliquent bêtement un symbole qui n’a de sens que dans le corps des réels !
L’objection des vulgarisateurs se présente ainsi : i² = √(-1)√(-1)= √((-1)(-1) = 1 d’où la prétendue contradiction.
Pourtant, des auteurs d’une grande réputation (Richard Feynman et Roger Penrose par exemple), n’hésitent pas à écrire i =√(-1) ! Mais dans ce cas, et bien qu’effectivement une telle expression est formellement incorrecte, ils veulent simplement et par raccourci, écrire que la racine carrée de -1 est égale à i dans le corps des complexes.
Précisons bien que la racine carrée de 4 est ±2 alors que √(4) = 2 par définition du symbole √ dont le résultat se limite toujours à la racine positive.
Or, le concept de nombre positif et négatif n’existe pas dans le corps des nombres complexes !. Par conséquent, le symbole √, qui ne donne que la racine positive, n’a aucun sens dans le corps des complexes.
Mais tout rentre dans l’ordre si on écrit i = -11/2 et on a bien
i² =-11/2 -11/2 = -11/2+1/2 = -1
Et c’est parfaitement cohérent ! (rappel : La racine carrée d’un nombre n, réel ou complexe, peut s’écrire : n½, n étant strictement positif dans le cas des réels)
En effet, écrivons –11/2 = e1/2log(-1) (car ab =eblog(a) e est la base des logarithmes népériens (*))
Or, log(-1) = iπ (**)
d’où –11/2 = e1/2log(-1) = eiπ/2
Mais eiπ/2 = cos(π /2) + isin(π/2) = 0 + 1 car cos(π /2) = 0 et sin(π/2) =1
D’où finalement : –11/2 = i et i est bel et bien la racine carrée de -1 !
(*) e = 2.718…..)
(**) Rappel de la formule d’Euler : eiπ = -1 d’où log(-1) =iπ pour la même raison que, dans les logarithmes décimaux, donc à base 10, on a, par exemple :
103 = 1000, alors log(1000) = 3.
Moralité : Méfiez-vous comme de la peste des mauvais vulgarisateurs. Surtout de ceux qui prétendent vulgariser une science invulgarisable : La mécanique quantique sans mathématiques.
Merci de votre attention.
Cordialment.
Modifié en dernier par ptoléméee le 23 Jan 2020, 07:33, modifié 1 fois.
Re: Sur la racine carrée de i.
C'est une blague ?
Pourquoi) ne serait pas
ne serait pas 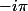 ? On n'a pas
? On n'a pas =-1) ?
?
Un conseil en passant : quand tu écris des exposants, si tu ne veux pas utiliser LaTeX, mets au moins un ^ pour rendre tes formules lisibles. Par exemple a^b pour a puissance b.
Pourquoi
Un conseil en passant : quand tu écris des exposants, si tu ne veux pas utiliser LaTeX, mets au moins un ^ pour rendre tes formules lisibles. Par exemple a^b pour a puissance b.
Re: Sur la racine carrée de i.
Bonjour,
Bien sûr que e^ -iπ = -1 puisque e^-iπ = cos(-iπ) + isin(-iπ) ! Mais je me suis borné à donner le résultat habituel.
Quant à mes formules, elles étaient parfaitement lisibles sous word.
En effet, les polices Ariel et Times Roman contiennent tous les symboles mathématiques et l'alphabet grec dont on ne peut se passer en mathématiques et en physique.
Je regrette que les textes écrits dans ces polices soient déformés lors de leur édition sur le forum.
Or, je n'ai pas du tout l'intention d'apprendre une nouvelle façon de rédiger mes expressions mathématiques.
Tant pis. Au temps pour moi.
Cordialement.
P.S. Je n'ai pas compris où est la blague. Voilà qui débuterait mal si j'avais l'intention de continuer.
Bien sûr que e^ -iπ = -1 puisque e^-iπ = cos(-iπ) + isin(-iπ) ! Mais je me suis borné à donner le résultat habituel.
Quant à mes formules, elles étaient parfaitement lisibles sous word.
En effet, les polices Ariel et Times Roman contiennent tous les symboles mathématiques et l'alphabet grec dont on ne peut se passer en mathématiques et en physique.
Je regrette que les textes écrits dans ces polices soient déformés lors de leur édition sur le forum.
Or, je n'ai pas du tout l'intention d'apprendre une nouvelle façon de rédiger mes expressions mathématiques.
Tant pis. Au temps pour moi.
Cordialement.
P.S. Je n'ai pas compris où est la blague. Voilà qui débuterait mal si j'avais l'intention de continuer.
Re: Sur la racine carrée de i.
Or, je n'ai pas du tout l'intention d'apprendre une nouvelle façon de rédiger mes expressions mathématiques.
La question est de savoir si tu t'exprimes sur un forum dans le but d'être compris. Si ce n'est pas le cas, continue d'écrire des formules illisibles, pas de problème ...
Sur le sujet :
"La" racine carrée d'un nombre complexe n'est pas bien définie, elle n'est définie qu'au signe près ; un nombre complexe non nul a deux racines carrées. "Le" logarithme d'un nombre complexe non nul n'est pas bien défini, il n'est défini qu'à
Re: Sur la racine carrée de i.
Vous ne m'apprenez rien !
Je crois que vous vous êtes polarisé sur un détail parfaitement correct dans le contexte, car il s'agissait EN FAIT essentiellement de l'écriture donnant comme la valeur -1 sous le radical à l'unité imaginaire i. ce qui est une erreur d'écriture.
Je persiste à ne pas comprendre en quoi mon texte correct pourrait être une blague.
Il est bien connu que les log complexes sont très riches en solutions, ce qui se révèle précieux plus tard.
Aussi, en bon VRAI scientifique avec plus de soixante ans de pratique de la mathématique et de la physique, je ne vois aucune utilité d'accepter des polémiques stériles, en dehors du sujet traité de surcroît, dès mon inscription à ce forum.
Aussi, déçu, j'arrête là totalement mes interventions.
Bien à vous.
Je crois que vous vous êtes polarisé sur un détail parfaitement correct dans le contexte, car il s'agissait EN FAIT essentiellement de l'écriture donnant comme la valeur -1 sous le radical à l'unité imaginaire i. ce qui est une erreur d'écriture.
Je persiste à ne pas comprendre en quoi mon texte correct pourrait être une blague.
Il est bien connu que les log complexes sont très riches en solutions, ce qui se révèle précieux plus tard.
Aussi, en bon VRAI scientifique avec plus de soixante ans de pratique de la mathématique et de la physique, je ne vois aucune utilité d'accepter des polémiques stériles, en dehors du sujet traité de surcroît, dès mon inscription à ce forum.
Aussi, déçu, j'arrête là totalement mes interventions.
Bien à vous.
Re: Sur la racine carrée de i.
tout rentre dans l’ordre si on écrit i = -11/2
Quand quelqu'un écrit que
en bon VRAI scientifique avec plus de soixante ans de pratique de la mathématique et de la physique
Inutile de jouer à l'argument d'autorité avec moi. Je ne suis pas en position d'être influencé par un tel argument.
Re: Sur la racine carrée de i.
Bonjour et adieu
Je ne puis rester sans réagir à votre propos un peu top hâtif !
Notations : R(n) désignera le radical. * désignera un produit.
Soit alors i² = -1. Donc i = R(-1)
Donc : i² = R(-1)*R(-1) (évident, non ?)
On a alors : R(-1)*R(-1) = R(-1*-1) = R(1) = 1 donc i² =1 !!! d'où la contradiction.
Si il y a une blague dans mon texte, elle est là, et c'est justement cette blague que j'ai dénoncée.
Et c'est cette blague que vous défendez implicitement.
A peine arrivé sur ce forum et plein de bonnes intentions, j'y suis immédiatement agressé.
Cela me suffit, ayant le désir bien légitime de vivre en paix sans être agressé gratuitement,
Vous perdrez votre temps en vous obstinant à me provoquer car je ne répondrai plus pour la bone raison que je ne reviendrai jamais plus sur ce forum que votre intervention a rendu si décevant.
Bien à vous
.
Je ne puis rester sans réagir à votre propos un peu top hâtif !
Notations : R(n) désignera le radical. * désignera un produit.
Soit alors i² = -1. Donc i = R(-1)
Donc : i² = R(-1)*R(-1) (évident, non ?)
On a alors : R(-1)*R(-1) = R(-1*-1) = R(1) = 1 donc i² =1 !!! d'où la contradiction.
Si il y a une blague dans mon texte, elle est là, et c'est justement cette blague que j'ai dénoncée.
Et c'est cette blague que vous défendez implicitement.
A peine arrivé sur ce forum et plein de bonnes intentions, j'y suis immédiatement agressé.
Cela me suffit, ayant le désir bien légitime de vivre en paix sans être agressé gratuitement,
Vous perdrez votre temps en vous obstinant à me provoquer car je ne répondrai plus pour la bone raison que je ne reviendrai jamais plus sur ce forum que votre intervention a rendu si décevant.
Bien à vous
.
Re: Sur la racine carrée de i.
Et c'est cette blague que vous défendez implicitement.
Absolument pas. La blague, je le répète, c'est de prétendre comme tu le fais que
si
Tu t'attendais peut-être à être reçu comme le messie. Désolé, mais il vaut mieux ne pas venir sur un forum si on ne supporte pas la critique.
Re: Sur la racine carrée de i.
Juste un petit détail : a^b*a^c = a^(b+c)
Donc -1^(1/2)*-1^1/2 = -1^(1/2+1/2) = -1^1 = -1.
Et, dans ce cas, on ne tombe pas sur une contradiction. Je n'ai rien voulu montrer d'autre !
Je ne me prends pas, et ne me suis jamais pris pour un messie. Encore une agression gratuite.
Au plaisir de ne plus vous lire.
Donc -1^(1/2)*-1^1/2 = -1^(1/2+1/2) = -1^1 = -1.
Et, dans ce cas, on ne tombe pas sur une contradiction. Je n'ai rien voulu montrer d'autre !
Je ne me prends pas, et ne me suis jamais pris pour un messie. Encore une agression gratuite.
Au plaisir de ne plus vous lire.
Re: Sur la racine carrée de i.
Il est tout aussi vrai que 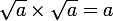 , donc
, donc 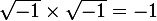 et on en tombe pas sur une contradiction. Du coup, ton argument ne fait pas avancer le schmilblick d'un poil et tu tournes en rond.
et on en tombe pas sur une contradiction. Du coup, ton argument ne fait pas avancer le schmilblick d'un poil et tu tournes en rond. 

Re: Sur la racine carrée de i.
Salut,
Si c'est juste GaBuZoMeu que tu ne veut "plus lire", je peut préciser que mon opinion est... exactement la même que lui.
Lorsque je lis tes différents post où il est écrit de multiple fois LA racine carrée où LE radical, ça donne l'impression que tu n'a pas bien compris la notion d'article défini/indéfini : pour pouvoir parler de LA racine d'un nombre complexe (et donc avoir le droit d'écrire
(et donc avoir le droit d'écrire 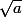 ) il faut qu'il y en ait UNE SEULE.
) il faut qu'il y en ait UNE SEULE.
Et vu que pour un complexe (non nul) donné il y a toujours deux solutions à l'équation
(non nul) donné il y a toujours deux solutions à l'équation 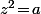 ça signifie qu'on ne risque pas de prendre uniquement
ça signifie qu'on ne risque pas de prendre uniquement 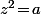 comme définition de LA racine carrée d'un complexe.
comme définition de LA racine carrée d'un complexe.
Je te rappelle quand même (au cas où...) qu'on voit normalement au collège que, dans l'ensemble des réels positifs, si on peut parler de LA racine carrée d'un nombre
d'un nombre  , ça provient du fait que si
, ça provient du fait que si 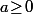 l'équation
l'équation 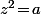 admet certes deux solutions (opposées l'une de l'autre) mais qu'elle n'en admet qu'une seule positive et c'est elle qu'on appelle LA racine carrée de
admet certes deux solutions (opposées l'une de l'autre) mais qu'elle n'en admet qu'une seule positive et c'est elle qu'on appelle LA racine carrée de  . En bref, c'est cette condition supplémentaire
. En bref, c'est cette condition supplémentaire 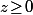 qui rend LA racine carrée unique et qui fait que, contrairement à ce que tu semble penser (*) , même pour des réels, le fait que
qui rend LA racine carrée unique et qui fait que, contrairement à ce que tu semble penser (*) , même pour des réels, le fait que 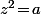 n'implique pas que
n'implique pas que 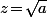 .
.
(*) c.f. début de ton post du 23 Jan 2020 09:49 où tu écrit " i² = -1. Donc i = R(-1)" qu'on peut compléter en écrivant qu'on a aussi (-i)² = -1 donc -i = R(-1) ce qui permet d'en déduire astucieusement que i = -i ...
Si c'est juste GaBuZoMeu que tu ne veut "plus lire", je peut préciser que mon opinion est... exactement la même que lui.
Lorsque je lis tes différents post où il est écrit de multiple fois LA racine carrée où LE radical, ça donne l'impression que tu n'a pas bien compris la notion d'article défini/indéfini : pour pouvoir parler de LA racine d'un nombre complexe
Et vu que pour un complexe
Je te rappelle quand même (au cas où...) qu'on voit normalement au collège que, dans l'ensemble des réels positifs, si on peut parler de LA racine carrée
(*) c.f. début de ton post du 23 Jan 2020 09:49 où tu écrit " i² = -1. Donc i = R(-1)" qu'on peut compléter en écrivant qu'on a aussi (-i)² = -1 donc -i = R(-1) ce qui permet d'en déduire astucieusement que i = -i ...
Modifié en dernier par Ben314 le 23 Jan 2020, 14:18, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Sur la racine carrée de i.
J'ai perdu mon message, mais en un mot : tout comme Ben, la notation ne change rien, le problème c'est l'unicité.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Sur la racine carrée de i.
Les problèmes concernant les racines carrées sont bien connus depuis Euler. Il y en avait d'autres, comme le fait que : √(1) = √((-1)×(-1)) = i×i = -1.
Comme tu l'as dit, tous ces problèmes sont dus au fait que chaque nombre réel ou complexe (à part quelques exceptions) possède deux racines carrées. Par exemple, √(4) = ±2 et √(-1) = ±i.
Pour lever l'ambiguité, il y a deux solutions.
La première est celle que l'on apprend dès le collège : pour les réels, on ne parle pas de racines carrées d'un nombre, mais de LA racine carrée d'un nombre en ne choisissant que la positive. idem dans les complexes, quand on écrit i = √(-1), il n'y a pas d'ambiguité, car les nombres i et -i sont indiscernables, remplacer l'un par l'autre ne modifie par les calculs algébriques (c'est l'une des bases de la théorie de Galois). Du coup, on a choisi par convention de noter i LA racine carrée de -1, ce qui revient à restreindre la fonction racine carrée sur les complexes à une seule de ses valeurs et à choisir une région du plan complexe où l'on découpe, où l'on passe de l'une à l'autre de ses déterminations.
La deuxième solution est de parler de fonctions multivaluées, c'est à dire un concept similaire à celui de fonction, mais pouvant admettre plusieurs images pour une valeur d'entrée donnée (on peut les voir comme des applications de l'ensemble d'entrée vers l'ensemble des parties de l'ensemble de sortie). A ce moment là, la racine carrée est une fonction multivaluée sur les complexes, dont les deux images sont opposées, mais aussi le logarithme est une fonction multivaluée sur les complexes, ou chaque valeur admet une infinité d'images toutes séparées par des multiples entiers de 2iπ. C'est cette position qui a été défendue par Euler pour lever les paradoxes concernant l'extension des fonctions racines et logarithmes.
Comme tu l'as dit, tous ces problèmes sont dus au fait que chaque nombre réel ou complexe (à part quelques exceptions) possède deux racines carrées. Par exemple, √(4) = ±2 et √(-1) = ±i.
Pour lever l'ambiguité, il y a deux solutions.
La première est celle que l'on apprend dès le collège : pour les réels, on ne parle pas de racines carrées d'un nombre, mais de LA racine carrée d'un nombre en ne choisissant que la positive. idem dans les complexes, quand on écrit i = √(-1), il n'y a pas d'ambiguité, car les nombres i et -i sont indiscernables, remplacer l'un par l'autre ne modifie par les calculs algébriques (c'est l'une des bases de la théorie de Galois). Du coup, on a choisi par convention de noter i LA racine carrée de -1, ce qui revient à restreindre la fonction racine carrée sur les complexes à une seule de ses valeurs et à choisir une région du plan complexe où l'on découpe, où l'on passe de l'une à l'autre de ses déterminations.
La deuxième solution est de parler de fonctions multivaluées, c'est à dire un concept similaire à celui de fonction, mais pouvant admettre plusieurs images pour une valeur d'entrée donnée (on peut les voir comme des applications de l'ensemble d'entrée vers l'ensemble des parties de l'ensemble de sortie). A ce moment là, la racine carrée est une fonction multivaluée sur les complexes, dont les deux images sont opposées, mais aussi le logarithme est une fonction multivaluée sur les complexes, ou chaque valeur admet une infinité d'images toutes séparées par des multiples entiers de 2iπ. C'est cette position qui a été défendue par Euler pour lever les paradoxes concernant l'extension des fonctions racines et logarithmes.
Notre chaîne youtube de mathématiques : https://www.youtube.com/c/QuadriviuumTremens
Re: Sur la racine carrée de i.
GaBuZoMeu a écrit:Il est tout aussi vrai que, donc
et on en tombe pas sur une contradiction. Du coup, ton argument ne fait pas avancer le schmilblick d'un poil et tu tournes en rond.
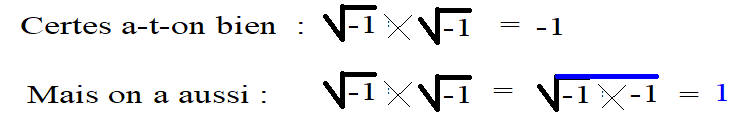
Mais j'ai lu ceci :
http://www.micmaths.com/blog/index.php? ... acine-de-1
Re: Sur la racine carrée de i.
Encore une fois, puisque tu n'as pas l'air de comprendre mon objection principale (ce n'est pourtant pas faute de la répéter) :
L'utilisation de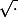 en dehors des réels positifs pose un certain nombre de problèmes dûs au fait qu'il n'y a pas d'application "racine carrée" sur le groupe multiplicatif des complexes qui soit un morphisme de groupes (contrairement à ce qui se passe sur le groupe multiplicatif des réels positifs).
en dehors des réels positifs pose un certain nombre de problèmes dûs au fait qu'il n'y a pas d'application "racine carrée" sur le groupe multiplicatif des complexes qui soit un morphisme de groupes (contrairement à ce qui se passe sur le groupe multiplicatif des réels positifs).
Ceci constaté, penser qu'il suffit de remplacer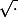 par
par ^{1/2}) pour que "tout rentre dans l'ordre", comme tu l'écris, me paraît de la plus haute fantaisie. Je l'ai écrit, je le maintiens, et je constate que tu ne réponds absolument pas sur ce point.
pour que "tout rentre dans l'ordre", comme tu l'écris, me paraît de la plus haute fantaisie. Je l'ai écrit, je le maintiens, et je constate que tu ne réponds absolument pas sur ce point.
L'utilisation de
Ceci constaté, penser qu'il suffit de remplacer
Re: Sur la racine carrée de i.
GaBuZoMeu a écrit:Encore une fois, puisque tu n'as pas l'air de comprendre mon objection principale (ce n'est pourtant pas faute de la répéter) :
L'utilisation deen dehors des réels positifs pose un certain nombre de problèmes dûs au fait qu'il n'y a pas d'application "racine carrée" sur le groupe multiplicatif des complexes qui soit un morphisme de groupes (contrairement à ce qui se passe sur le groupe multiplicatif des réels positifs).
Ceci constaté, penser qu'il suffit de remplacerpar
pour que "tout rentre dans l'ordre", comme tu l'écris, me paraît de la plus haute fantaisie. Je l'ai écrit, je le maintiens, et je constate que tu ne réponds absolument pas sur ce point.
Bonjour,
Je n'ai fait que signaler un contre exemple, contradictoire avec votre expression.
L'important est le site (qui me donne tort !) que j'ai signalé mais que vous ne commentez pas..
Pour ma part, je ne tiens pas absolument à avoir raison. Il y a trop longtemps que cette partie des mathématiques a cessé d'être mon centre d'intérêt.
De plus, je m'étais spécialisé, de par mes fonctions chez mon employeur (un géant de l'Informatique), dans la recherche en analyse numérique à une époque passionnante de pionniers où TOUT était à faire relativement à la recherche de méthodes de calculs sur ordinateurs (équa dif, intégrales, calcul matriciel, recherche opérationnelle, etc. le plus souvent appliqués à la physique). Je me souviens d'une certaine intégrale sextuple (équation de Beth et Salpeter) appliquée à la diffusion proton-proton pour un thésard de Normal sup'. Cela remonte aux années 50 et 60.
En retraite à 65 ans depuis 1992, j'ai continué à entretenir en mécanique quantique mes neurones mais iceux commencent à un peu renâcler si je leur demande trop.
Comme tout le monde, il m'est arrivé de me tromper. Ou bien je m'en apercevais le premier, auquel cas je reconnaissais immédiatement mon erreur, ou bien on me la signalait courtoisement sans la traiter de "blague", et je la reconnaissais tout autant !
Je reconnais sans complexe votre expertise en mathématique mais je regrette que cette expertise vous fasse défaut en délicatesse. (Signe des temps ?)
Bien à vous
Re: Sur la racine carrée de i.
hi,
Je me souviens que l'on peut chercher à résoudre dans C, z^3 = 1
Y-a-t-il une notation pour dire qu'on veut z = 1^{1/3}, avec ^ fonction multivaluée (cf QuadriviuumTremens ) qui donne bien (e^{2ikpi/3}, k = 0, 1, 2) (mais peut-être que le symbole ^ est malvenu, y en a-t-il un autre)
Deuxième question: Si on prend un tel opérateur C dans C^3, mettons r:Z -> {ensemble des z tq z^3=Z}, je pense souvent au calcul numérique type octave, où chaque fonction (ex cosinus) peut admettre un tableau (auquel cas, cos(arr)->arr, idem chaque element E du tableau est mappé par cos(E)), j'ai envie d'écrire:
(r(1))^3 = 1
où 1 est bien dans C et non C^3 comme si on avait de nouveau aggrégé car unicité de valeur pour revenir dans C. Ce genre de "trick"/simplification existe-t-il dans la nature ?
Je me souviens que l'on peut chercher à résoudre dans C, z^3 = 1
Y-a-t-il une notation pour dire qu'on veut z = 1^{1/3}, avec ^ fonction multivaluée (cf QuadriviuumTremens ) qui donne bien (e^{2ikpi/3}, k = 0, 1, 2) (mais peut-être que le symbole ^ est malvenu, y en a-t-il un autre)
Deuxième question: Si on prend un tel opérateur C dans C^3, mettons r:Z -> {ensemble des z tq z^3=Z}, je pense souvent au calcul numérique type octave, où chaque fonction (ex cosinus) peut admettre un tableau (auquel cas, cos(arr)->arr, idem chaque element E du tableau est mappé par cos(E)), j'ai envie d'écrire:
(r(1))^3 = 1
où 1 est bien dans C et non C^3 comme si on avait de nouveau aggrégé car unicité de valeur pour revenir dans C. Ce genre de "trick"/simplification existe-t-il dans la nature ?
la vie est une fête 
Re: Sur la racine carrée de i.
Bonjour fatal_error,
Je ne comprends pas grand chose à ta deuxième question.
Pour la première question, on peut toujours choisir une "détermination principale" du logarithme pour un nombre complexe non nul, ce qui revient à prendre une "détermination principale" de l'argument (l'argument est la partie imaginaire du logarithme). Habituellement on prend la détermination principale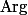 dans
dans 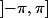 . À partir de là on a une détermination principale de
. À partir de là on a une détermination principale de 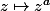 pour tout
pour tout 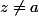 et tout réel
et tout réel  :
:  + i \mathrm{Arg}(z)\right)) . Ça vaut pour
. Ça vaut pour 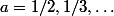 ; on peut même prendre
; on peut même prendre  complexe si ça nous chante.
complexe si ça nous chante.
Mais ceci ne règle pas le problème que j'ai déjà signalé de nombreuses fois et qui est la source du "paradoxe" de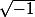 :
: 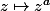 n'est pas un morphisme de groupe (on n'a pas
n'est pas un morphisme de groupe (on n'a pas ^a) ), contrairement à ce qui se passe quand on travaille sur les réels positifs.
), contrairement à ce qui se passe quand on travaille sur les réels positifs.
Je ne comprends pas grand chose à ta deuxième question.
Pour la première question, on peut toujours choisir une "détermination principale" du logarithme pour un nombre complexe non nul, ce qui revient à prendre une "détermination principale" de l'argument (l'argument est la partie imaginaire du logarithme). Habituellement on prend la détermination principale
Mais ceci ne règle pas le problème que j'ai déjà signalé de nombreuses fois et qui est la source du "paradoxe" de
Re: Sur la racine carrée de i.
GaBuZoMeu a écrit:Bonjour fatal_error,
Je ne comprends pas grand chose à ta deuxième question.
Pour la première question, on peut toujours choisir une "détermination principale" du logarithme pour un nombre complexe non nul, ce qui revient à prendre une "détermination principale" de l'argument (l'argument est la partie imaginaire du logarithme). Habituellement on prend la détermination principaledans
. À partir de là on a une détermination principale de
pour tout
et tout réel
:
. Ça vaut pour
; on peut même prendre
complexe si ça nous chante.
Mais ceci ne règle pas le problème que j'ai déjà signalé de nombreuses fois et qui est la source du "paradoxe" de:
n'est pas un morphisme de groupe (on n'a pas
), contrairement à ce qui se passe quand on travaille sur les réels positifs.
Mais ceci ne règle pas le problème que j'ai déjà signalé de nombreuses fois et qui est la source du "paradoxe" de
Eh bien, la voilà la bonne réponse ! (Je ne l'avais pas vue !)
Re: Sur la racine carrée de i.
Cette explication du fait qu'on n'a pas de morphisme de groupes était déjà dans ce message, puis répétée dans un message suivant ....
Sujet: Sur la racine carrée de i.
Mieux vaut tard que jamais
Sujet: Sur la racine carrée de i.
Mieux vaut tard que jamais
35 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
