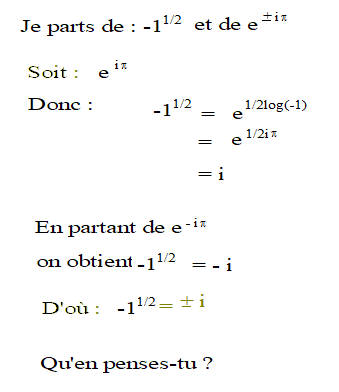Sur la racine carrée de i.

[ptoléméee]

Cette explication du fait qu'on n'a pas de morphisme de groupes était déjà dans ce message, puis répétée dans un message suivant ....
Sujet: Sur la racine carrée de i.
Mieux vaut tard que jamais

[ptoléméee]

Cette explication du fait qu'on n'a pas de morphisme de groupes était déjà dans ce message, puis répétée dans un message suivant ....
Sujet: Sur la racine carrée de i.
Mieux vaut tard que jamais

En déclarant ci-dessus que "je ne l'avais pas vue", je reconnais avoir eu tort.
Cela dit, vous n'avez pas répondu à ma demande de commenter cet article :
http://www.micmaths.com/blog/index.php? ... acine-de-1

De plus, des physiciens de l'envergure de Richard Feynman et Roger Penrose pour ne citer qu'eux ne se privent pas d'écrire le symbole "racine carrée de -1" !

[GaBuZoMeu]

Cela dit, vous n'avez pas répondu à ma demande de commenter cet article :
http://www.micmaths.com/blog/index.php? ... acine-de-1

Bof, pas terrible. Mickaël Launay est mieux inspiré sur pas mal d'autre sujets. Mon reproche principal est qu'il présente le choix de la racine carrée "principale" pour un nombre complexe comme une convention de même nature que le choix de la racine carrée positive pour un réel positif, alors que c'est profondément différent.

[Ben314]

Salut,
Personnellement, je trouve l'article "bof bof", c'est à dire pas franchement "faux", mais pas très utile à quoi que ce soit non plus : c'est très très long pour ne pas dire grand chose.
Ma vision des choses c'est la suivante (et c'est bien ce que l'on trouve délayé dans l'article) :
(1) Une notation, ben c'est rien d'autre qu'une notation et ça n'a aucun sens de dire qu'une notation est "vrai" ou "fausse". Une notation, ça peut être "pratique" ou "pas très pratique" (pour mener des calculs) et ça peut être "classique" (i.e. adopté par la majorité des matheux actuels) ou au contraire "atypique".
Concernant la notation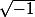 , elle n'est pas très pratique car plus longue à écrire que la simple lettre (ou pour les physiciens) et elle est éventuellement sources d'erreurs pour des matheux débutants (voir le point 2). De plus, à l'heure actuelle, elle est plutôt atypique. Par contre, historiquement parlant, la notation a été longtemps utilisée (j'ai la flemme de chercher qui a utilisé pour la première fois la lettre à la place de , mais c'est assez récent). Donc on peut, si on aime la polémique, discuter le coté "atypique" de cette notation.
(2) En temps que prof. de math., j'ai souvent enseigné les nombres complexes à des étudiants et j'ai effectivement souvent prononcé/écrit la fameuse phrase "il n'y a pas de racine carrée sur C" (donc pas de racine carrés de -1) sans trop rentrer dans les détails vu le niveau (très basique) des étudiants auquel je m'adressait. Comme le fait remarquer l'article que tu cite, cette phrase, telle quelle, est fausse : on peut parfaitement définir une (ou plutôt des) fonction(s) racine carrée sur C. Ce qui n'existe pas, c'est un morphisme de groupe multiplicatif, c'est à dire une fonction racine carrée telle que, pour tout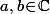 , on ait 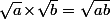. Et c'est à cause de cette propriété "défaillante" que la plupart des pédagogues (et pas la plupart des matheux) considèrent qu'il est dangereux de laisser des matheux débutant utiliser des racines carrées de complexes. De plus, dans le supérieur, ce chapitre sur les nombres complexes se termine très souvent par un paragraphe sur " les racines n-ièmes" (en particuliers les racines n-ièmes de l'unité) qui constituent une notion importante en mathématique et vu que durant ce paragraphe on parle à longueur de temps DES racines n-ièmes d'un complexe donné, pédagogiquement parlant, ça semble raisonnable d'inciter les étudiants dés le départ à ne parler que DES racines carrés d'un complexe et jamais de LA racine d'un complexe.
Bref, tout ça pour dire que, pédagogiquement parlant, je suis on ne peut plus favorable à ce que l'on interdise l'utilisation du symbole racine carré avec les complexes lors de l'apprentissage "basique" des complexes.
Bien évidement, une fois que les étudiants ont un peu plus de maturité et sont donc capable de comprendre le problème, rien n’empêche de "lever le tabou". Par exemple la majorité des profs. et bouquins de L3 / M1 ne se gênent absolument pas pour parler de l'anneau .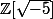

[ptoléméee]

Salut,
Personnellement, je trouve l'article "bof bof", c'est à dire pas franchement "faux", mais pas très utile à quoi que ce soit non plus : c'est très très long pour ne pas dire grand chose.
Ma vision des choses c'est la suivante (et c'est bien ce que l'on trouve délayé dans l'article) :
(1) Une notation, ben c'est rien d'autre qu'une notation et ça n'a aucun sens de dire qu'une notation est "vrai" ou "fausse". Une notation, ça peut être "pratique" ou "pas très pratique" (pour mener des calculs) et ça peut être "classique" (i.e. adopté par la majorité des matheux actuels) ou au contraire "atypique".
Concernant la notation , elle n'est pas très pratique car plus longue à écrire que la simple lettre (ou pour les physiciens) et elle est éventuellement sources d'erreurs pour des matheux débutants (voir le point 2). De plus, à l'heure actuelle, elle est plutôt atypique. Par contre, historiquement parlant, la notation a été longtemps utilisée (j'ai la flemme de chercher qui a utilisé pour la première fois la lettre à la place de , mais c'est assez récent). Donc on peut, si on aime la polémique, discuter le coté "atypique" de cette notation.
(2) En temps que prof. de math., j'ai souvent enseigné les nombres complexes à des étudiants et j'ai effectivement souvent prononcé/écrit la fameuse phrase "il n'y a pas de racine carrée sur C" (donc pas de racine carrés de -1) sans trop rentrer dans les détails vu le niveau (très basique) des étudiants auquel je m'adressait. Comme le fait remarquer l'article que tu cite, cette phrase, telle quelle, est fausse : on peut parfaitement définir une (ou plutôt des) fonction(s) racine carrée sur C. Ce qui n'existe pas, c'est un morphisme de groupe multiplicatif, c'est à dire une fonction racine carrée telle que, pour tout , on ait . Et c'est à cause de cette propriété "défaillante" que la plupart des pédagogues (et pas la plupart des matheux) considèrent qu'il est dangereux de laisser des matheux débutant utiliser des racines carrées de complexes. De plus, dans le supérieur, ce chapitre sur les nombres complexes se termine très souvent par un paragraphe sur " les racines n-ièmes" (en particuliers les racines n-ièmes de l'unité) qui constituent une notion importante en mathématique et vu que durant ce paragraphe on parle à longueur de temps DES racines n-ièmes d'un complexe donné, pédagogiquement parlant, ça semble raisonnable d'inciter les étudiants dés le départ à ne parler que DES racines carrés d'un complexe et jamais de LA racine d'un complexe.
Bref, tout ça pour dire que, pédagogiquement parlant, je suis on ne peut plus favorable à ce que l'on interdise l'utilisation du symbole racine carré avec les complexes lors de l'apprentissage "basique" des complexes.
Bien évidement, une fois que les étudiants ont un peu plus de maturité et sont donc capable de comprendre le problème, rien n’empêche de "lever le tabou". Par exemple la majorité des profs. et bouquins de L3 / M1 ne se gênent absolument pas pour parler de l'anneau .

Bonjour et merci !
On ne peut qu'apprécier une telle mise au point énoncée sans aucune hostilité. ni formule méprisante.
J'avoue, lors de mon texte initial avoir été trop négligent, négligence due en grande partie au fait qu'il y a au moins une bonne vingtaine d'années que je ne me suis penché sur les complexes que d'un point de vue de la physique, notamment, entre autres, dans le cadre de la fonction d'onde en mécanique quantique.
Donc, je reconnais, la honte au front, m'être fourvoyé imprudemment dans un domaine en grande partie oublié.
Cordialement.

[mathelot]

(j'ai la flemme de chercher qui a utilisé pour la première fois la lettre à la place de

c'est Euler me semble-t-il

[GaBuZoMeu]

Bon, ptolémée, je t'ai froissé en parlant de "blague". Mais :
1°) ton âge vénérable fait que tu as peut-être un épiderme un peu trop sensible aux vannes qu'on peut envoyer sur un forum ;
2°) relis ton premier message, et dis moi sincèrement : rétrospectivement, vu ce qui s'en est suivi, ne trouves-tu pas qu'il a un ton légèrement prétentieux ? En tout cas, je l'ai ressenti comme tel.

[ptoléméee]

Bon, ptolémée, je t'ai froissé en parlant de "blague". Mais :
1°) ton âge vénérable fait que tu as peut-être un épiderme un peu trop sensible aux vannes qu'on peut envoyer sur un forum ;
2°) relis ton premier message, et dis moi sincèrement : rétrospectivement, vu ce qui s'en est suivi, ne trouves-tu pas qu'il a un ton légèrement prétentieux ? En tout cas, je l'ai ressenti comme tel.

Bonjour,
Pour moi, la "blague" est oubliée.
L'âge ne saurait en aucun cas être une excuse pour une erreur commise. Cette erreur, je l'ai reconnue sans ambiguïté.
Ma réaction n'a pas été épidermique. Ainsi que je l'ai déjà mentionné, il m'est arrivé parfois (sinon souvent) de commettre des erreurs, erreurs que j'ai toujours reconnues sans complexe .
Que mon message ait pu paraître prétentieux est une erreur profonde. A la rigueur pourrais-je admettre une certaine maladresse.
Tout ceci m'a quand même rendu un fier service : Je m'aperçois, à ma grande confusion, qu'importante est ma perte de mémoire dans certains domaines mathématiques.. J'en tiendrai compte à l'avenir.
Je dois néanmoins rappeler que j'ai dû très tôt, pour des raisons professionnelles, me reconvertir vers l'analyse numérique, discipline beaucoup plus compliquée que l'on pourrait croire. Surtout à la naissance des ordinateurs où TOUT était à trouver.
Cordialement.

[GaBuZoMeu]

Loin de moi l'idée que l'analyse numérique c'est de la gnognotte.

[ptoléméee]

Loin de moi l'idée que l'analyse numérique c'est de la gnognotte.

Bonjour,
Petit retour en arrière.

[GaBuZoMeu]

Que a deux racines carrées dans . Ce n'est pas vraiment un scoop. Où veux-tu en venir ?
Je pense que la situation est claire. Pourquoi continuer à tourner autour du pot ?

[Ben314]

Le passage par les logarithmes ne change rien au problème :
De la même façon qu'on a de gros soucis à définir la racine d'un complexe du fait que l'équation 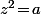admet plusieurs solutions (à savoir deux), ben on a exactement le même problème pour définir le logarithme d'un complexe du fait que l'équation admet plusieurs solutions (à savoir une infinité).
Par exemple, l'équation a pour solution tout les qui sont LES logarithmes de -1 et il n'y a aucune raison particulière de privilégier l'une de ces solution pour en faire LE logarithmes de -1. Bien sûr, comme pour la racine carrée, on peut privilégier une des solutions (par exemple l'unique solution dont la partie imaginaire est dans 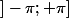) et affirmer que c'est cette solution là que l'on va appeler LE logarithme de . Sauf que,exactement comme pour la racine carré, en privilégiant une des solutions, on perd la propriété caractéristique des logarithmes, à savoir que ce qui rend la fonction beaucoup beaucoup moins utile que dans .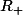
Bref, concernant ton ln(-1), TU as choisi de dire qu'il était égal à +i mais il faut bien comprendre que c'est parfaitement arbitraire et que tu aurais tout aussi bien pu décider de prendre ln(-1)=-i, voire ln(-1)=2021i si ça t'amuse. Et bien évidement, la valeur que tu va trouver pour va dépendre du choix (arbitraire) que tu as fait concernant "qui" est .

[ptoléméee]

Que a deux racines carrées dans . Ce n'est pas vraiment un scoop. Où veux-tu en venir ?
Je pense que la situation est claire. Pourquoi continuer à tourner autour du pot ?

Je voulais simplement montrer que de -1 puissance 1/2 émerge i come étant sa valeur.
C'est tout.

[ptoléméee]

Le passage par les logarithmes ne change rien au problème :
De la même façon qu'on a de gros soucis à définir la racine d'un complexe du fait que l'équation admet plusieurs solutions (à savoir deux), ben on a exactement le même problème pour définir le logarithme d'un complexe du fait que l'équation admet plusieurs solutions (à savoir une infinité).
Par exemple, l'équation a pour solution tout les qui sont LES logarithmes de -1 et il n'y a aucune raison particulière de privilégier l'une de ces solution pour en faire LE logarithmes de -1. Bien sûr, comme pour la racine carrée, on peut privilégier une des solutions (par exemple l'unique solution dont la partie imaginaire est dans ) et affirmer que c'est cette solution là que l'on va appeler LE logarithme de . Sauf que,exactement comme pour la racine carré, en privilégiant une des solutions, on perd la propriété caractéristique des logarithmes, à savoir que ce qui rend la fonction beaucoup beaucoup moins utile que dans .
Bref, concernant ton ln(-1), TU as choisi de dire qu'il était égal à +i mais il faut bien comprendre que c'est parfaitement arbitraire et que tu aurais tout aussi bien pu décider de prendre ln(-1)=-i, voire ln(-1)=2021i si ça t'amuse. Et bien évidement, la valeur que tu va trouver pour va dépendre du choix (arbitraire) que tu as fait concernant "qui" est .

Bien d'accord avec tout ça !
Mais, comme je l'indique ci-dessus, j'ai simplement voulu montrer un exemple que de -1 puissance 1/2 émerge spontanément i dans le cas le plus simple.

[ptoléméee]

Le passage par les logarithmes ne change rien au problème :
De la même façon qu'on a de gros soucis à définir la racine d'un complexe du fait que l'équation admet plusieurs solutions (à savoir deux), ben on a exactement le même problème pour définir le logarithme d'un complexe du fait que l'équation admet plusieurs solutions (à savoir une infinité).
Par exemple, l'équation a pour solution tout les qui sont LES logarithmes de -1 et il n'y a aucune raison particulière de privilégier l'une de ces solution pour en faire LE logarithmes de -1. Bien sûr, comme pour la racine carrée, on peut privilégier une des solutions (par exemple l'unique solution dont la partie imaginaire est dans ) et affirmer que c'est cette solution là que l'on va appeler LE logarithme de . Sauf que,exactement comme pour la racine carré, en privilégiant une des solutions, on perd la propriété caractéristique des logarithmes, à savoir que ce qui rend la fonction beaucoup beaucoup moins utile que dans .
Bref, concernant ton ln(-1), TU as choisi de dire qu'il était égal à +i mais il faut bien comprendre que c'est parfaitement arbitraire et que tu aurais tout aussi bien pu décider de prendre ln(-1)=-i, voire ln(-1)=2021i si ça t'amuse. Et bien évidement, la valeur que tu va trouver pour va dépendre du choix (arbitraire) que tu as fait concernant "qui" est .

Bien d'accord avec tout ça !
Mais, comme je l'indique ci-dessus, j'ai simplement voulu montrer un exemple que de -1 puissance 1/2 émerge spontanément i dans le cas le plus simple.

Je comprends bien qu'il en est de même avec i puissance i qui est égal, dans sa solution la plus immédiate à 0.208879.....
Ce résultat est un cas particulier d'une multitude d'autres obtenus en le multipliant par exp(2pin) avec n entier.